1.题目:必修2《直线与平面垂直的判定》片段教学
2.内容:

3.基本要求:
(1)试讲10分钟
(2)需有师生互动环节
(3)适当结合板书
(4)理解线面垂直的判定定理
【试题解析】
一、创设情景,揭示课题
(一)教师首先提出问题:在现实生活中,我们经常看到一些直线与平面垂直的现象,例如:“旗杆与地面,大桥的桥柱和水面等的位置关系”,你能举出一些类似的例子吗?然后让学生回忆、思考、讨论、教师对学生的活动给予评价。
(二)接着教师指出:一条直线与一个平面垂直的意义是什么?并通过分析旗杆与它在地面上的射影的位置关系引出课题内容。
二、探究新知
(一)为使学生学会从“感性认识”到“理性认识”过程中获取新知,可再借助长方体模型让学生感知直线与平面的垂直关系。然后教师引导学生用“平面化”的思想来思考问题:从直线与直线垂直、直线与平面平行等的定义过程得到启发,能否用一条直线垂直于一个平面内的直线来定义这条直线与这个平面垂直呢?并组织学生交流讨论,概括其定义。
如果直线L与平面α内的任意一条直线都垂直,我们就说直线L与平面α互相垂直,记作L⊥α,直线L叫做平面α的垂线,平面α叫做直线L的垂面。如图,直线与平面垂直时,它们唯一公共点P叫做垂足。并对画示表示进行说明。
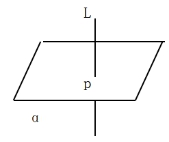
(二)教师提出问题,让学生思考:
1、问题:虽然可以根据定义判定直线与平面垂直,但这种方法实际上难以实施。有没有比较方便可行的方法来判断直线和平面垂直呢?
2、师生活动:请同学们准备一块三角形的纸片,我们一起来做如下图的试验:过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触),问如何翻折才能保证折痕AD与桌面所在平面垂直?

3、归纳结论:引导学生根据直观感知及已有经验(两条相交直线确定一个平面),进行合情推理,获得判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
教师特别强调:1)定理中的“两条相交直线”这一条件不可忽视;2)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想。
三、巩固深化
课本P69例1
四、归纳小结
小结:采用师生对话形式,完成下列问题:
1、请归纳一下获得直线与平面垂直的判定定理的基本过程。
2、直线与平面垂直的判定定理,体现的教学思想方法是什么?
五、课后作业
思考题:如果一条直线垂直于平面内的无数条直线,那么这条直线就和这个平面垂直,这个结论对吗?为什么?
六、板书设计
直线与平面垂直的判定

一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
1.题目:必修1《函数的奇偶性》片段教学
2.内容:
3.基本要求:
(1)试讲约10分钟;
(2)渗透数形结合等数学思想;
(3)要有讨论环节,
(4)要有适当板书。
【试题解析】
一、展示图片,悬疑导入
多媒体展示喜字、蝴蝶、扑克牌、交通标志四幅图片,请学生观察这些图片具有什么样的共同特征。
通过观察,老师适当引导,学生能够发现前两幅图是轴对称的,后两幅图是中心对称的。
继续追问数学中这样的对称,请学生举例说明。由于前几节课都在学习函数,会有部分学生想到有些函数的图象是对称的。引入课题:今天我们一起来研究图象具有对称特征的函数的性质——奇偶性
二、合作探究,新课讲授
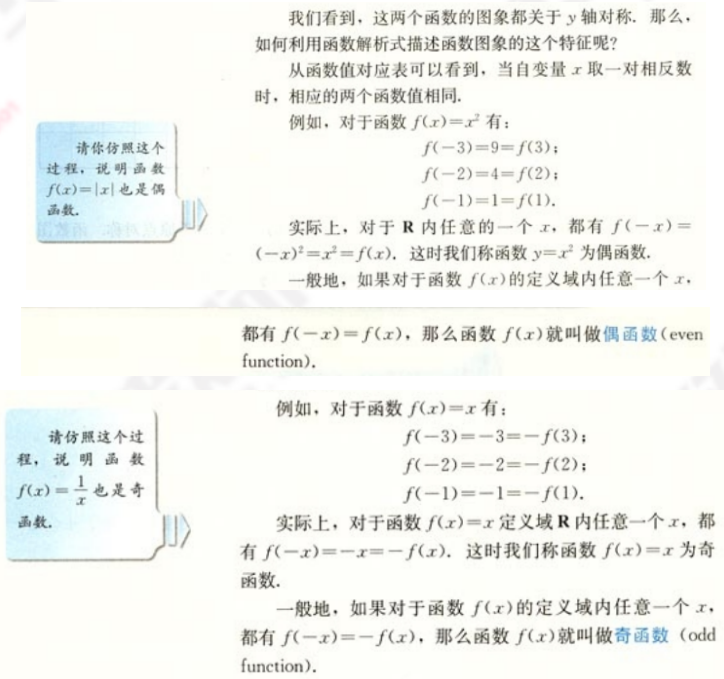
(一)偶函数
1.观察下列函数的图象:说明图象有什么样的特点。


(学生讨论完成,要求学生说明理由。)
四、回顾整理,反思提升
通过今天的实际应用,大家有哪些收获呢,可以说一说,知识上的,方法上的,数学思想上的,等等都行。
引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识的归纳,纳入自己的知识结构。
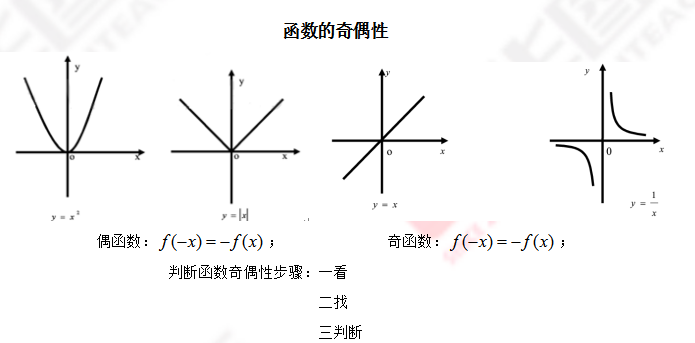
师生一起回顾函数奇偶性的定义,图象性质,以及如何判断一个函数的奇偶性。
五、知识拓展,布置作业
1.完成课后习题1题;
2.思考函数奇偶性的应用,下节课一起展示分享。
板书设计:
1.题目:选修2-2《类比推理》片段教学
2.内容:

3.基本要求:
(1)试讲约10分钟;
(2)由生活实际中的类比推理引入数学中的类比推理;
(3)根据教学内容适当板书。
【试题解析】

1.题目:选修一《椭圆及其标准方程》片段教学
2.内容:

3.基本要求:
(1)试讲约10分钟;
(2)理解椭圆的定义;
(3)思路清晰,逻辑性强
(4)配合教学内容适当板书。
【试题解析】

1.题目:必修五《正弦定理的应用》片段教学
2.内容:

3.基本要求:
(1)试讲约10分钟;
(2)渗透分类导论的思想;
(3)配合教学内容适当板书。
【试题解析】

题目1:平行公理
题目2:不等式性质2
题目3:不等式的性质5

最后,华图教师希望各位考生能够努力学习、积极备考、持之以恒、克服困难,早日圆教师梦想!
文章来源于中国教师资格网










