2020安徽省考行测练习之数量关系：数学运算(7.23)

　1.

　　

　　A.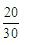

　　B.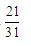

　　C.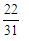

　　D.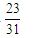

　　2.某单位举办活动，需要制作8米长的横幅20条。用来制作横幅的原料有两种，一种每卷10米，售价10元;另一种每卷25米，售价23元。如果每卷原料截断后无法拼接，则该单位购买横幅原料最少需要花费( )元。

　　A.146

　　B.158

　　C.161

　　D.200

　　3.在1000以内，除以3余2，除以7余3，除以11余4的数有多少个?

　　A.4

　　B.5

　　C.6

　　D.7

　　4.不等式组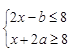中x的最大解区间为[-2,1]，则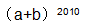的值为( )。

　　A.0

　　B.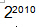

　　C.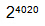

　　D.1

　　5.如果把一个体积为125立方厘米的正方体铁块切割成体积相等的8个小正方体，则每个小正方体铁块的表面积是( )。

　　A.6.25平方厘米

　　B.15.625平方厘米

　　C.16.5平方厘米

　　D.37.5平方厘米

　　ღ答案在下一页👇

　　

　　答案与解析

　　1.答案: B

　　解析:

　　原式=1/31+(2×101)/(31×101)+(5×10101)/(31×10101)+(13×1010101)/(31×1010101)=1/31+2/31+5/31+13/31=21/31。故正确答案为B。

　　2.答案: B

　　解析:

　　每卷10米的只能制作一条横幅，因此相当于单价为10元;每卷25米的只能制作三条条幅，因此相当于单价为23/3<10元。因此要制作20条横幅，购买方式为每卷25米的购买6卷，每卷10米的购买2卷，花费为23×6+10×2=158元。故正确答案为B。

　　3.答案: B

　　解析:

　　解析一：此题不属于余同、差同及和同问题，属于周期问题，有余数出现即为不完全周期问题。先从“除以7余3，除以11余4”入手，寻找满足“除以7余3，除以11余4”的周期。此数可写成：x=7a+3或者x=11b+4，(a、b为正整数)即x=7a+3=11b+4，不难得出满足等式的最小整数x=59，同时59满足"除以3余2”这个三位数可写成3×7×11n+59，n可以取0、1、2、3、4，答案选B。

　　解析二：同余问题，不符合“余同取余，和同加和，差同减差，最小公倍数做周期”的口诀，通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17，其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意：0≤231n+59≤1000，解得0≤n≤4。所以这样的数共有5个，故正确答案为B。

　　口诀解释：余同取余，例如“一个数除以7余1，除以6余1，除以5余1”，可见所得余数恒为1，则取1，被除数的表达式为210n+1;和同加和，例如“一个数除以7余1，除以6余2，除以5余3”，可见除数与余数的和相同，取此和8，被除数的表达式为210n+8;差同减差，例如“一个数除以7余3，除以6余2，除以5余1”，可见除数与余数的差相同，取此差4，被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。

　　4.答案: D

　　解析: 解不等式组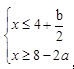，，则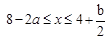，根据解区间，得a=5,b=-6，代入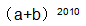，得原式=1.本题答案为D选项。

　　5.答案: D

　　解析:

　　此题目的关键在于计算得出每个小正方体铁块的边长，每个小正方体的体积为：125÷8=125/8 立方厘米，则每个小正方体铁块的边长为5/2 厘米，因此每个小正方体铁块的表面积为：6×5/2×5/2=6×25/4=37.5 平方厘米，故正确答案为D。