2021年公务员考试每日练习:数量关系(10月13日)
1.
一列客车长250米,一列货车长350米,在平行的轨道上相向行驶,从两车头相遇到两车尾相离经过15秒,已知客车与货车的速度比是5:3。问两车的速度相差多少?( )
A.10米/秒
B.15米/秒
C.25米/秒
D.30米/秒
2.
某市组织技术人员到外地培训学习,需要先乘车再乘船才能到达目的地。要保证每个人都有座位,需要每辆有60个座位的大巴至少4辆,需要定员为70人的船至少3条。到达目的地之后,对技术人员进行分组培训,结果发现,分的组数跟每组的人数恰好相等、则参加这次培训学习的技术人员共有( )名。
A.169
B.181
C.196
D.225
3.
﹣2,﹣1,1,5,( )
A.12
B.13
C.14
D.15
4.
如下图所示,梯形 ABCD,AD∥BC,DE⊥BC,现在假设 AD、BC 的长度都减少 10%,DE 的长度增加 10%,则新梯形的面积与原梯形的面积相比,会怎样变化?( )
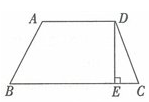
A.不变
B.减少 1%
C.增加 10%
D.减少 10%
5.1,32,81,64,25,( ),1
A.5
B.6
C.10
D.12
答案与解析1.答案: A
解析:
>两车头相遇到两车尾相离相当于两车车尾相遇过程,设两车速度为5v、3v,则有15×(5v+3v)=250+350,解得v=5,因此两车速度相差5v-3v=2v=10米/秒。
2.答案: C
解析:
解法一:代入排除法,“分的组数跟每组的人数恰好相等”可知人员数是一个平方数,排除B,代入A、C、D人员数除以60结果大于3小于4,除以70结果大于2小于3,计算所得只有196符合条件。故答案选C。
解法二:设参加这次培训学习的技术人员共有x名,由题意知,180<x≤240,140<x≤210,>整理,得>180<x≤210>。排除>AD>,又分的组数跟每组的人数恰好相等,排除B>。故本题答案选>C>。
注意:题干中的要求:“要保证每个人都有座位”
3.答案: B
解析:
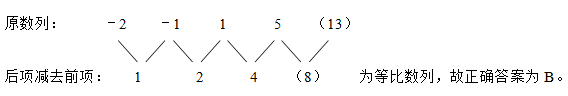
4.答案: B
解析:
设AD=x,BC=y,DE=z,那么梯形面积为z(x+y)/2,经过变形后梯形面积为1.1z(0.9x+0.9y)/2=0.99z(x+y)/2,即比原梯形面积少1%。故正确答案为B。
5.答案: B
解析: 1,32,81,64,25,( ),1,为幂次数列,把原数列变为幂次数形式为:1^6,2^5,3^4,4^3,5^2,( ),7^0,因此选项为6^1=6,因此,本题答案选择B选项。










