2021年公务员考试每日练习：数量关系（11月17日）

　　1.

　　已知甲溶液的浓度为46%，乙溶液的浓度为32%，第一次取两种溶液混合后浓度变为40.4%。第二次取的每种溶液比第一次混合的量都多10升，再混合后浓度变为40%，那么第二次混合时，乙溶液取了多少升?( )

　　A.12

　　B.30

　　C.36

　　D.42

　　2.　　

　　A.x=1

　　B.x=1999

　　C.x=2000

　　D.x=2001

　　3.

　　A.7

　　B.10

　　C.12

　　D.11

　　4.

　　5，16，29，45，66，94( )

　　A.114

　　B.121

　　C.133

　　D.142

　　5.某班56名学生参加了奥数或作文课外兴趣小组的活动，其中参加奥数的有32人，参加作文的有35人，问两种活动都参加的有多少人?( )

　　A.3

　　B.11

　　C.21

　　D.24

　　答案与解析1.答案: B

　　解析:

　　根据十字交叉法，可知第一次混合的甲乙溶液比为(40.4%-32%)：(46%-40.4%)=3：2，第二次混合的甲乙溶液比为(40%-32%)：(46%-40%)=4：3，容易看出第二次多取的10升表示的恰好是“1”份，因此第二次混合所取的乙溶液为10×3=30(升)。

　　2.答案: D

　　解析:　　

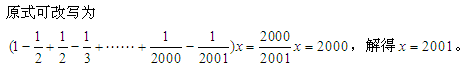
　　因此正确答案为D。

　　3.答案: D

　　解析: 上网6.7小时按7小时计费。不超过4小时的部分收费4X2=8(元)，超过4小时的部分收费(7-4)X1=3(元)，所以小米共花费8+3=11(元)。故选D。

　　4.答案: C

　　解析:

　　原数列经过两次做差之后得到质数列。

　　5.答案: B

　　解析: 本题考查基本的二集合容斥原理。由两集合标准型核心公式：两种活动都参加的人数=参加奥数的人数+参加作文的人数-总人数=(32+35)-56=11。因此，本题答案为B选项。