想必在所有公考人的心中,对于图形推理一定都是又爱又恨的。爱在它有意思、出题形式活,具有一定的挑战性;恨在短时间内又很难掌握其做题的精髓和技巧,从而难得高分。不论如何,图形推理都是公考路上如磐石一样屹立不倒的存在,那我们如何去攻克它呢?除了刷题之外,其实更重要的是需要将所刷的题进行有效总结,整理出相同或相似考查形式下所涉及的各类考点,以便在考前进行系统梳理,从而全面掌握图形的各个考点,实现高分目标!
图形推理在历年考试试题中对于黑白块的考查均是重点,频次也非常之高,近几年更是打破了传统的平移和黑白运算的单一考法,融合了很多其他形式,出题点愈发灵活了。比如说从黑白块的样式上进行叠加或者求同求异等,或者从黑块的数量和面积上进行考查,甚至会从黑白块的相互分割作用上入手,具有很大的创新性。下面是对于近年来关于黑白块的各种考点进行的总结:
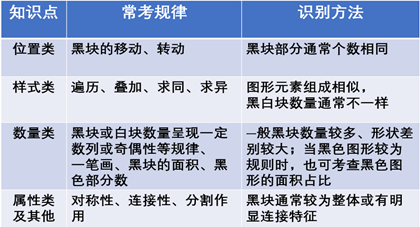
上述表格中,不仅有关于黑白块的各种常考规律的总结,同时,为了防止大家只能领会表面的皮毛,而不能真正掌握识别这些规律的技巧,所以还专门附带了识别方法,帮助大家在面对不同的出题形式时能够快速进行考点定位,从而在短时间安内做出正确答案。下面通过思维导图的方式将遇到黑白块时的整体思路进行完整梳理:

下面,我们就通过一道真题运用这一思路解答一下:
【例】从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:
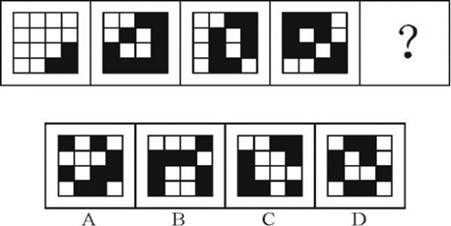
【答案】D
【解析】图形中出现小黑块,观察各图小黑块的个数,除了第一个图之外,后面的图均存在较多的小黑块,因此考虑黑块的整体性。观察发现各图中小黑块均连在一起整体出现,所以考虑优先考虑黑块较为整体时的几个常考考点。由于各图中通过小黑块的连接将白色部分分割成了1、2、3、4份,所以问号处需要黑块将白色部分分成5份,只有D项符合,因此答案选D。
综上,我们在做图形题时如果遇到了黑白块则可以通过上述思路来进行考点的定位,从而更快速地做出正确答案。当然这些不同的考点可能还会在未来的考试中不断进行创新和融合,因此大家在对这些考点进行熟记的基础上还应多在真题中通过训练不断补充和总结,以更充实和全面的知识点掌握来应对考试。










