数量关系在我们行测考试中一直处于难点,特别是在遇到排列组合问题以及行程问题时,很多考生感到困难,但是在行程问题中也有一些看到关键词就想起并利用公式就能解出答案的题目,今天就来给大家介绍行程问题中的等距离平均速度的公式以及如何求解,希望大家看完后面的讲解能够有所收获,能在考试中多多得分。

一、等距离平均速度公式推导。
![]()
我们知道求平均速度是等于总路程除以总时间,既然距离相等,便可以设两个距离均为S,设第一段路的速度为,第二段路的速度为,要求平均速度,根据总路程除以总时间可得。
二、等距离平均公式使用情况。
等距离平均公式使用条件必须满足要求平均速度的两段路距离相等,因此当题目中出现类似于往返,前半段路后半段路,或者往返上下坡等表示两段路距离相等的情况下求两段路的平均速度即可使用。并且从公式中我们可以看出没有路程S出现,因此求平均速度与路程无关,大家在解题过程中不要受到题目中路程等无关因素的干扰。
三、例题精讲。
【例1】小王上山速度为60米/分钟,原路返回的速度为100米/分钟,问小王往返的平均速度是多少米/分钟?( )
A.85 B.80

C.75 D.90

【答案】C 解析:本题要求解小王往返的平均速度,从题目中可以看到往返速度不同,但是路程相等,再看问题求平均速度,故可以使用等距离平均速度的公式直接求解。列式可得米/分钟,故本题选C选项。
【例2】小明每天从家中出发骑自行车经过一段平路,再经过一道斜坡后到达学校上课。某天早上,小明从家中骑车出发,一到校门口就发现忘带课本,马上返回,从离家到赶回家中共用了1个小时,假设小明当天平路骑行速度为9千米/小时,上坡速度为6千米/小时,下坡速度为18千米/小时,那么小明的家距离学校多远?
A.3.5千米 B.4.5千米

C.5.5千米 D.6.5千米
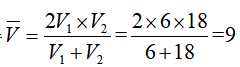
【答案】B解析:本题要求的是小明家到学校的距离,但是并不知道平路以及上下坡所花的时长,因此没办法利用一般的公式求解,但是根据题意,小明从家到学校进行往返运动,因此上下坡距离相等,可考虑利用等距离平均速度求得千米/小时,由于平路速度也为9千米/小时,往返总时间是1小时,故往返总路程为9×1=9千米,则小明的家距离学校9÷2=4.5千米。因此,选择B选项。
相信通过上面两个例题的讲解分析,大家对等距离平均速度的用法有了更进一步的了解,当读完一个题目,看到往返,上下坡,前一半后一半等这类词在行程问题中出现,就要考虑等距离平均速度去进行解题,打开自己的思路。










