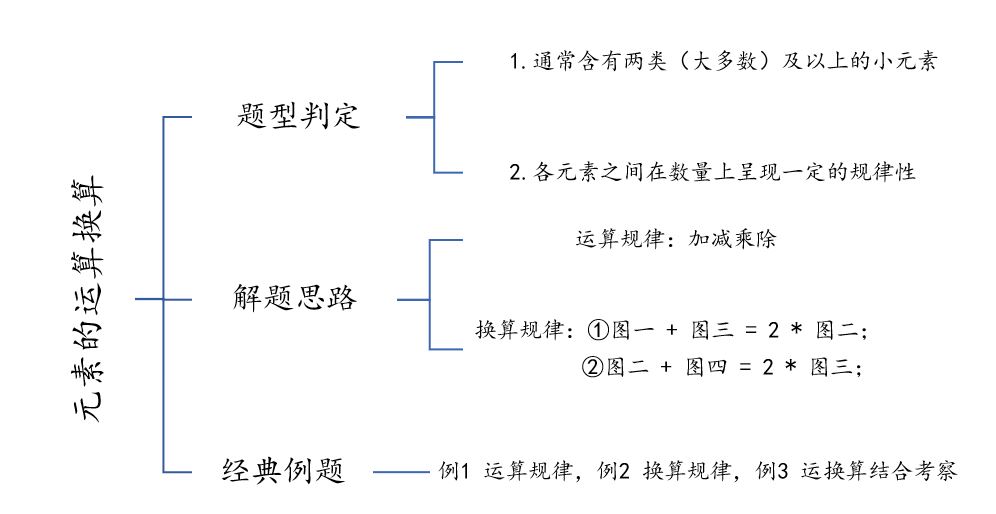
数量类的考点一直是考试中的重难点,而当题目涉及到元素运换算时会让难度更上一层楼,如何轻松拿下这类题目,华图老师将带着大家一起来探讨学习下元素的运换算专项。
(一)题型判定
观察图形整体元素组成不同,进一步观察这类题型通常含有两类(大多数)及以上的小元素,各元素之间在数量上呈现一定的规律性。
(二)解题思路
这类题目通常考察元素之间的运换算规律,做题时,可将题目当中的小元素进行简单罗列,再找出运换算关系。
常考的两大考点:
(1)运算规律:图形当中元素之间的基本运算,常考的是加、减。
(2)换算规律:两种小元素按照一定比例换算之后总数量呈现数量规律,常考的是等差规律,极少考察等比规律。在这里给大家提供两种常用的换算方法:
=1*GB3①图一+图三=2*图二;
=2*GB3②图二+图四=2*图三;
接下来,我们通过历年真题来梳理下考点。
(三)经典例题
1.从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:
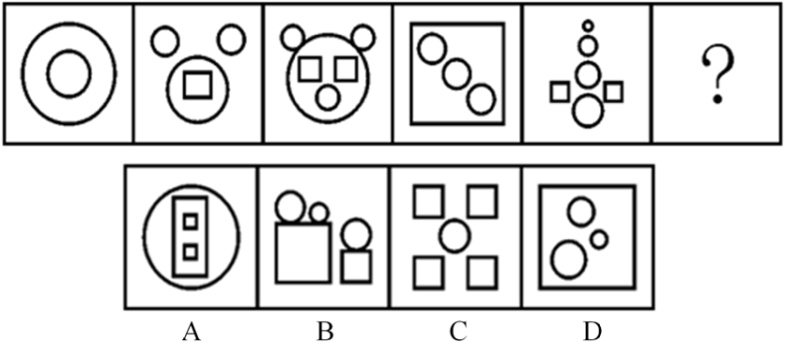
【答案】D
观察特征,组成元素不同,图形当中均由两种元素组成,且数量变化明显,考点元素的运换算规律。一条式,从左到右找规律。分开数圆形和矩形的个数,如下表所示,规律为○-□=2,只有D项符合。

【拓展】本题考查元素运算规律。当图形由两种元素构成时,建议分开数个数,考虑各组数字本身或者两组数字间运算或换算的规律。
2.从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:
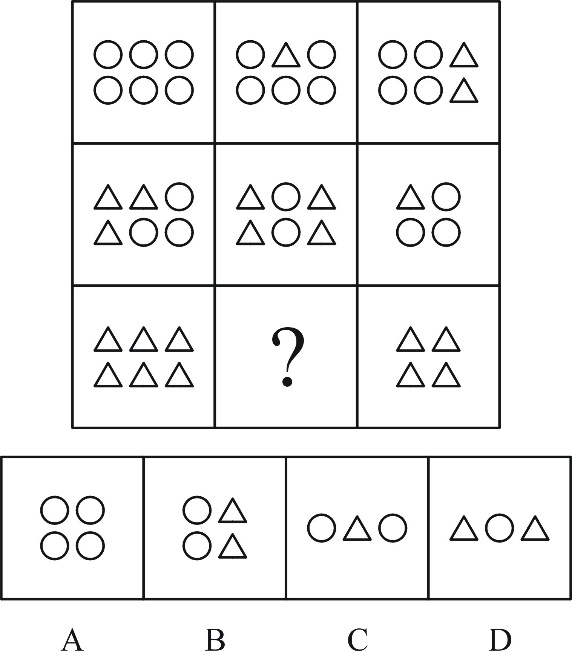
【答案】C
这道题目是陕西2018年的省考题目,先观察特征。组成元素不同,图形当中由圆形和三角形组成,考虑元素的运换算规律。元素之间无运算规律,考虑换算规律。九宫格,横向规律较为常见,优先考虑。先看第一行,利用图1+图3=2*图2,得到一个恒等公式,再看第二行,得到换算公式:1○=2△。将公式代入原图得三角形个数,第一行依次是12、11、10;第二行依次为9、8、7;第三行依次为6、?、4;符合等差规律,因此问号处三角形个数应该为5个,只有C项符合。
【拓展】本题考查元素的换算规律
3.从四个选项中选择一个替代问号,使两套图形的规律表现出最大的相似性,最适合的是()
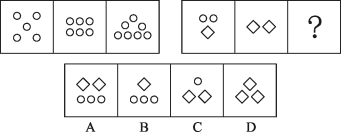
【答案】C
本题是2020年深圳市考的一道题目,与上述两道题目不同或者说更难得点在于,这道题目综合了元素的运算和换算规律双考点。
观察特征。图形组成不同,题干小元素居多,考虑元素考点,两段式,第一段找规律,第二段用规律。第一段,图形中圆的数量分别为5、6、7,呈递增的等差规律;第二段出现两种元素,两种元素之间无运算规律,考虑换算,应用第一段规律,可得换算规律◇=3○,则换算后前两图中圆的数量分别为5、6,问号处换算后应有7个圆,只有C项符合。因此,选择C选项。
【拓展】本题考查元素的运算和换算规律
通过对历年真题的梳理,相信不少同学对元素的运换算考察有所掌握。在这里给各位考生一些建议,同学们除了日常的刷题外,一定要善于总结和梳理,才能让公考之路事半功倍。