分段打折不复杂,列表对比搞定它
利润问题是三支一扶行测中的一个高频考点,其中的分段打折问题在考试中往往占用考生大量的时间,那么如何在考试中更快做出这类题目呢?今天华图教育给大家分享一个小技巧:列表对比不同方案下商品打折情况,进而快速计算结果。
在学习分段打折问题之前,我们需要先掌握打折问题会涉及的三个基本公式:

下面我们一起来看两道分段打折题目:
例1
某商场做促销活动,一次性购物不超过500元的打九折优惠;超过500元的,其中500元打九折优惠,超过500元部分打八折优惠。小张购买的商品需付费490元,小李购买的商品比原价优惠了120元。如两人一起结账,比分别结账可节省多少元钱?
A.10 B.20 C.30 D.50
【答案】D。解析:方法一:要求一起结账比分别结账可节省的钱,需求解出一起结账的总价和分别结账的总价。首先需要知道小张和小李分别购买时商品的原价:
根据“一次性购物不超过500元的打九折优惠”可知,如果原价刚好是500元,则折后价应该为500×0.9=450元。而小张付费为490元>450元,则小张的原价应超过500元,且超过500元的部分其折前价为(490-450)÷0.8=50元,所以小张的原价应该为500+50=550元。
同理,如果小李的原价刚好是500元,打九折即优惠了500元的10%:500×0.1=50元。根据“小李购买的商品比原价优惠了120元”可知,小李的原价中超出500元的部分优惠了120-50=70元。因此超出500元的部分其折前价为70÷(1-0.8)=350元,所以小李的原价为500+350=850元。
因此,两人商品的原价总和为550+850=1400元,可得两人一起结账的价格为500×0.9+(1400-500)×0.8=1170元。而两人分别结账的价格总和为490+(850-120)=1220元。所以可节约1220-1170=50元。选D选项。
方法一通过基础公式求解题目,但是因为考试的时间比较紧张,求解过程就稍显复杂,下面我们给大家分享另外一种更为快速的方法。
方法二:通过分段计算规则可知,两人的原价都是超过500元的,且享受的优惠情况如下表所示:
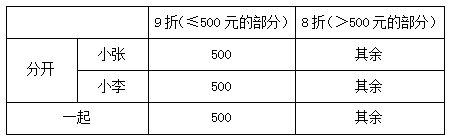
通过列表我们会发现,两人分开结账时,有2个500元打了9折,其余的钱都打了8折。而两人一起结账时,只有1个500元打了9折,其余的钱都打了8折,也就是说有1个500元从原本打9折变成了打8折,因此优惠的钱=500×(0.9-0.8)=50元,选D选项。
例2
某商店实行打折销售,顾客消费在100元以内的部分,按8折收费,超过100元的部分按6折收费。小王购物第一次付款56元,第二次又付款98元。如果他一次购买并付款,可以节省多少元?
A.10 B.12 C.14 D.16
【答案】C。解析:如果一次性购买100元的商品,只需要付款100×0.8=80元。小王第一次付款56元<80元,因此第一次的原价为56÷0.8=70元。第二次付款金额98元>80元,则第二次的原价应大于100元,两次享受的优惠情况如下表所示:

从表中可以看出分开购买时,一共有170元打8折,其余6折;而如果一起购买,只有100元打8折,其余6折。也就是说有70元从原本打8折变成了打6折,因此可节省的钱=70×(0.8-0.6)=14元,选C选项。
总结:在求解利润问题中的分段打折问题时,一定要弄清楚每个分段的优惠方式和购买原价,通过列表分析对比出单独买和合并买时每个分段的打折情况,找到两种购买方式下折扣不一样的部分,就能算出两者的差值。










