题型：单选题（分值：1）

　　连接大正方形的一条对角线，将正方形分成了两个三角形。在两个三角形内分别画出正方形X、Y（如下图所示）。那么，X与Y的面积之比为多少？

　　A.9∶8

　　B.8∶7

　　C.7∶6

　　D.1∶1

　　答案：A

　　解析：

　　第一步，本题考查几何问题，属于平面几何类。

　　第二步，如图，因为X为正方形，OE垂直于AD、OF垂直于CD，故三角形AEO和CFO均为等腰直角三角形。则AE=EO=ED、CF=OF=DF，得到E、F是正方形边长的中点。故X的面积==，即大正方形面积的。

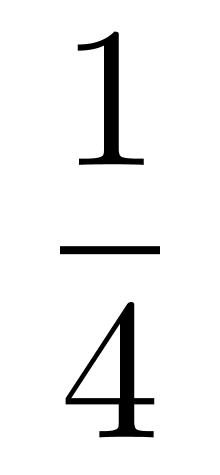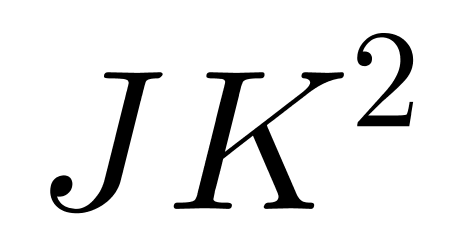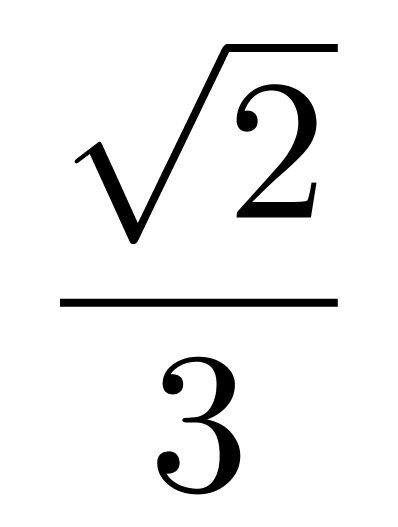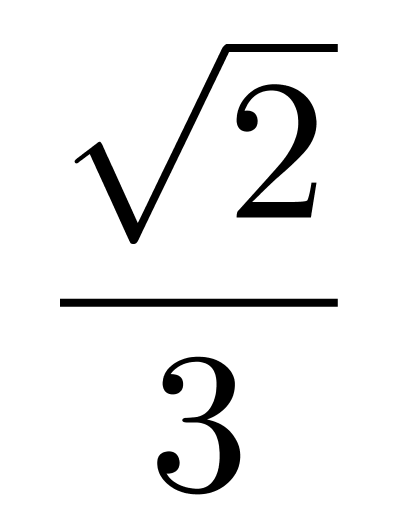　　第三步，同理三角形AHJ和CIK均为等腰直角三角形，得到AJ=HJ=JK=CK，则J、K为对角线AC的两个三等分点。根据勾股定理得到AC=AD，得到Y的面积==AD×AD=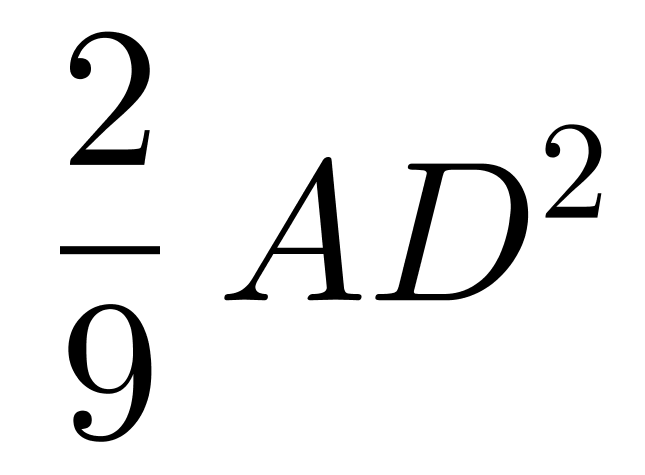，即大正方形面积的。

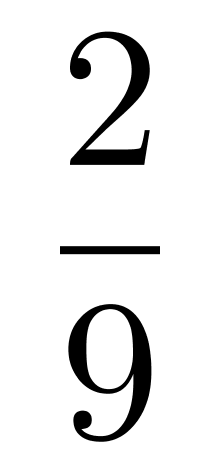　　第四步，故X和Y两者之间的面积比=∶=9∶8。

　　因此，选择A选项。

　　来源：2024年国家公务员考试行测模考第十二季

　　以上是的试卷的部分试题内容，更多2024年国考,国家公务员考试,国考行测模考，请继续查看2024年国家公务员考试行测模考第十二季试题题库或最新国考试题题库。