1.(单选题)某单位开展“我身边的榜样”评选活动,现对3名候选人甲、乙、丙进行不记名投票,投票要求详见选票。这3名候选人的得票数(不考虑是否有效)分别为总票数的88%、70%、46%,则本次投票的有效率(有效票数与总票数的比值)最高可能为:

A.68%
B.88%
C.96%
D.98%
解析
第一步,本题考查最值问题,属于其他最值构造。
第二步,设总共有100人投票,则共投出了88+70+46=204(次)选票,每张选票“○”的个数不超过2时才为有效票,为了使有效票率高,只需无效票尽量少,故先让100人每人投出两票,共100×2=200票,则剩余204-200=4票,则无效票最少有4张,故有效票最多有100-4=96票,本次投票的有效率最高可能为96%。
因此,选择C选项。
2.(单选题)某个正方形剧场院子每边的外墙长度都是100米,15点整甲和乙两名保安同时从同一个角出发反向而行,分别以每分钟60米和80米沿着院子的外墙巡逻,15点9分30秒到15点10分30秒之间,甲和乙之间最短的直线距离应:
A.小于50米
B.在50~75米
C.在75~100米
D.大于100米
解析
第一步,本题考查几何问题,属于平面几何类。
![]()
第二步,如下图所示,甲、乙从A点出发,反向而行,15点9分30秒时,二人走过的时间为9.5分钟。甲走过的路程为9.5×60=570(米),走过了一圈在距C点30米的E,乙走过的路程为9.5×80=760(米),差40米就回到原点,在距A点40米的H。15点9分30秒到15点10分30秒间,甲、乙分别走了60米和80米,那么这段时间内,甲会在C点两侧各30米的EF之间行走,乙会在A点两侧各40米的GH之间行走。二者之间最短的直线距离为EH=FG=(米),且明显小于100,可见此数在75—100米之间。
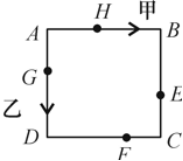
因此,选择C选项。
3.(单选题)某围棋队的两位选手小李与小张决定进行1次围棋比赛,两人轮流先手开局,第一局小李先手开局。甲、乙两人分别记录了全程比赛,均显示共比赛18局,结果为10∶8。甲的记录显示为:小李胜10局,小张胜8局,且先手者共胜8局,但乙的记录显示为:先手者共胜6局。问甲乙两人的记录结果是:
A.甲错乙对
B.甲错乙错
C.甲对乙错
D.甲对乙对
解析
第一步,本题考查比赛问题。
第二步,设小李先手开局时胜x局,根据小李共胜10局,则小李执后手时胜(10-x)局。共比赛18局,则小李共9局为执后手,则小李执后手时共输9-(10-x)=(x-1)局,即小张先手开局共赢(x-1)局,可得先手者共胜x+(x-1)=(2x-1)局,根据奇偶性可知,先手者共胜局数为奇数,则甲、乙两人记录结果均错误。
因此,选择B选项。
4.(单选题)一辆垃圾转运车和一辆小汽车在一段狭窄的道路上相遇,必须其中一车倒车让道才能通过,已知小汽车倒车的距离是转运车的9倍,小汽车的正常行驶速度是转运车的3倍,如果小汽车倒车速度是其正常速度的六分之一,垃圾转运车倒车速度是正常速度的五分之一,问应该由哪辆车倒车才能够使两车尽快都通过?
A.小汽车
B.垃圾转运车
C.两车均可
D.无法计算
解析
第一步,本题考查行程问题。
第二步,赋值狭窄道路全长300,则小汽车需要倒车距离(转运车需要前进距离)为270,转运车需要倒车距离(小汽车需要前进距离)为30。赋值小汽车的正常速度为30,则小汽车倒车速度为5,转运车正常速度为10,转运车倒车速度为2。
第三步,若小汽车倒车,在小汽车倒车的过程中,转运车可继续前进,当小汽车倒车结束时,转运车已完成前进任务,需要时间为270÷5+300÷30=64;若转运车倒车,在转运车倒车的过程中,小汽车可继续前进,当转运车倒车结束时,小汽车已完成前进任务,需要时间为30÷2+300÷10=45。故转运车倒车更省时,能使两车都尽快通过。
因此,选择B选项。
5.(单选题)下列图形中,阴影部分面积为2的是:
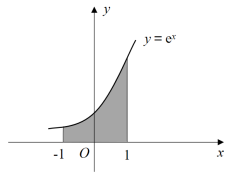
A.
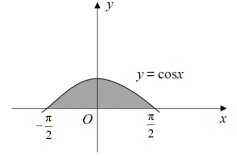
B.
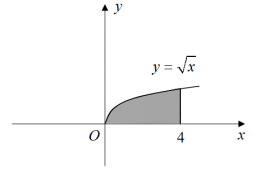
C.
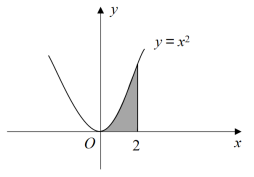
D.
解析
第一步,本题考查定积分的应用。
第二步,曲边梯形面积的计算,采用定积分来解题。
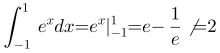
A选项,,A选项错误;
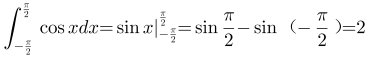
B选项,,B选项正确;
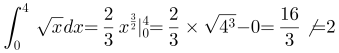
C选项,,C选项错误;
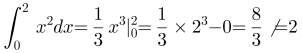
D选项,,D选项错误。
因此,选择B选项。
6.(单选题)某企业生产一批产品,计划在42天内完成。先由甲、乙车间共同生产,12天后甲车间完成总任务的10%,乙车间完成总任务的15%。乙车间因设备整修,此后只能以80%的效率工作。为按时完成任务,丙车间此时新加入工作。问其产能至少应是甲车间的:
A.100%
B.80%
C.60%
D.50%
解析
第一步,本题考查工程问题。
第二步,由12天后甲车间完成总任务的10%,可得甲车间完成任务需要120天,由12天后乙车间完成总任务的15%,可得乙车间完成任务需要80天,赋值工程总量为240,那么甲车间的效率为2,乙车间的效率为3,合作12天完成(2+3)×12=60,工程还剩240-60=180,计划42天完成,还剩42-12=30(天),乙车间的效率变为3×80%=2.4。
![]()
第三步,设丙的效率为x,可列方程:(2+2.4+x)×30=180,解得x=1.6,那么丙车间的产能是甲的=80%。
因此,选择B选项。
7.(单选题)某方舱医院配有1000张床位,现已接收新冠确诊患者200名,并按床护比(护士数与床位数的比值)0.6:1配齐了护士人员。因疫情发展迅速,该医院又收治了700名患者,此时床护比下调为0.2:1,那么还需增加护士:
A.80人
B.60人
C.40人
D.20人
解析
第一步,本题考查基础应用题。
第二步,接收患者200人时,护士与床位的比值为0.6:1,此时护士120人。后来又增加了700名患者,共900名,护士与床位的比值为0.2:1,此时需要护士的总数为180人,需要增加180-120=60名。
因此,选择B选项。
8.(单选题)某公司职员预约某快递员上午9点30分到10点在公司大楼前取件,假设两人均在这段时间内到达,且在这段时间到达的概率相等。约定先到者等后到者10分钟,过时交易取消。快递员取件成功的概率为:
![]()
A.
![]()
B.
![]()
C.
![]()
D.
解析
第一步,本题考查概率问题,用图像法解题。
第二步,两人相差不超过10分钟到达可交易成功,取特殊值确定图像。
①职员9:30到,快递员在9:30—9:40之间到即可;
②职员9:40到,快递员在9:30—9:50之间到即可;
③职员9:50到,快递员在9:40—10:00之间到即可;
④职员10:00到,快递员在9:50—10:00之间到即可。
可绘制出如下图像:
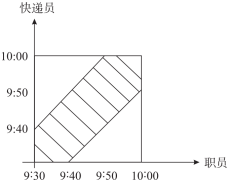
![]()
那么阴影部分占总数的1-×××2=。
因此,选择C选项。
9.(单选题)小伟参加英语考试,共50道题,满分为100分,得60分算及格。试卷评分标准为做对一道加2分。做错一道倒扣2分,结果小伟做完了全部试题但没及格。他发现,如果他少做错两道题就刚好及格了。问小伟做对了几道题?
A.32
B.34
C.36
D.38
解析
解法一:
第一步,本题考查基础应用题,用方程法解题。
第二步,设做对x道题,由少做错2道刚好及格,可得如果答对(x+2)道题,可得60分;又由于他做了全部的题目,所以如果及格说明他做错了(50-x-2)道题。于是有2(x+2)-2(50-x-2)=60,解得x=38。
因此,选择D选项。
解法二:
第一步,本题考查基础应用题。
![]()
第二步,试卷满分100分,每少做对1道题,少得4分(做了全部题目)。由少做错2道刚好及格可知,小伟得分为52分,即少得100-52=48(分)。所以他做错了(道)题目,做对了50-12=38(道)。
因此,选择D选项。
10.(单选题)三位运动员跨台阶,台阶总数在100~150级之间,第一位运动员每次跨3级台阶,最后一步还剩2级台阶。第二位运动员每次跨4级台阶,最后一步还剩3级台阶。第三位运动员每次跨5级台阶,最后一步还剩4级台阶。则这些台阶总共有( )级。
A.119
B.121
C.129
D.131
解析
解法一:
第一步,本题考查余数问题,用代入排除法解题。
第二步,由每次跨3级剩2级可知,台阶总数减去2能被3整除,排除B、C选项;由每次跨5级剩4级可知,台阶总数减去4能被5整除,排除D选项。
因此,选择A选项。
解法二:
第一步,本题考查余数问题。
第二步,若台阶多一级,则台阶总数可以被3、4、5同时整除,因此原台阶总数可表示为60n-1(60为3、4、5的最小公倍数)。
第三步,台阶数在100~150级之间,只有当n=2时,总数为60×2-1=119(级)在此区间。
因此,选择A选项。










