题型：单选题（分值：1）
如下图所示，AB是圆的直径，C、D分别是圆周上的两点，已知圆的半径是10cm，C点到AB的垂直距离是5cm，CD=12cm，若在直径AB上存在一个点F到C、D两点之间的距离和最短，那么该最短距离是多少厘米？
A.
B.
C.16
D.20
答案：B
解析：
第一步，本题考查平面几何问题。
第二步，如下图作辅助线，作C点关于AB的对称点C′，连接C′D，C′D与AB的交点即为F点，F点到C、D两点的距离为DC′。点O为圆心，连接CO、C′O，且作CE垂直C′D于E点。
第三步，由C点到AB的距离是5cm，可知CC′=10cm，根据圆形的半径为10cm，可知?CC′O是等边三角形，因此∠COC′=60?。根据圆周角是圆心角的一半，可知∠CDC′=30?。在直角?CDE中，CD=12cm，∠CDE=30?，因此DE=
，CE=6。在直角?CEC′中，CE=6，CC′=10cm，根据勾股定理可得到EC′=
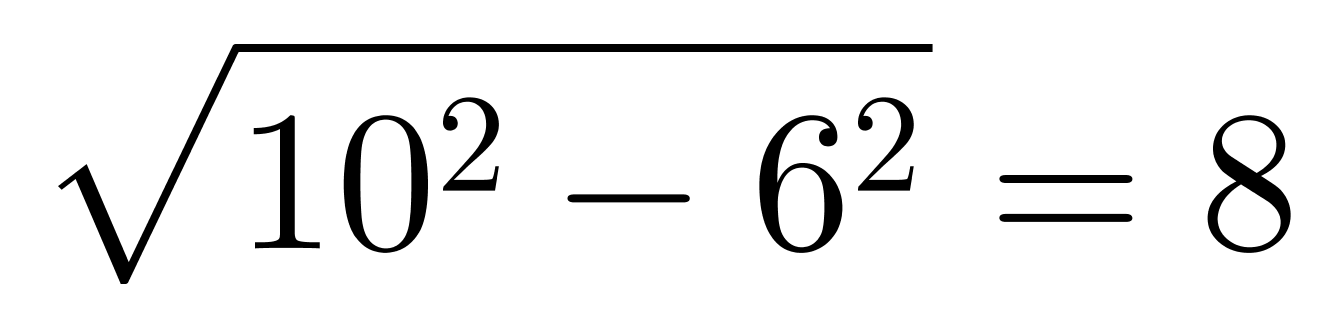。因此DC′=DE+EC′=
+8。
因此，选择B选项。
以上是的试卷的部分试题内容，更多2024年国考,国家公务员考试,国考行测模考，请继续查看2024年国家公务员考试行测模考第三十一季试题题库或最新国考试题题库。
