1.(单选题)地球绕太阳公转的周期为365天5小时48分46秒。为了弥补历法规定造成的一年365天与地球公转周期的时间差,每4年设立一个闰年,闰年共有366天,并每百年减去一个闰年。若地球绕太阳公转的周期为365天8小时,而历法规定每一年仍是365天,那么为了补足地球公转周期的时间差,需要每?设置一个闰年。
A.1年
B.2年
C.3年
D.4年
解析
第一步,本题考查星期日期问题。
第二步,若地球绕太阳公转的周期是365天8小时,普通的平年一年是365天的话,每三年会多出8×3=24小时,即一天,需要设置一个闰年。
因此,选择C选项。
2.(单选题)某新建高速公路中间隔离带绿化时,顺次种植2株蜀桧、3株刺柏、5株小叶女贞、3株大叶黄杨,按此循环,第2019株树木是什么?
A.蜀桧
B.刺柏
C.小叶女贞
D.大叶黄杨
解析
第一步,本题考查循环周期问题。
第二步,一个循环周期共有2+3+5+3=13(株)树木,2019÷13=155……4,可得155个周期后还剩余4株树,剩余的4株树木为2株蜀桧,2株刺柏,那么第2019株树木为刺柏。
因此,选择B选项。
3.(单选题)小许早上8:00从A地开车去B地取一批货物,他全程保持匀速并于11:00到达B地。在到达B地30分钟后,小许以比来时慢20千米/小时的速度驶回A地,并在行驶一半距离后恢复至原速度,并于15:00抵达A地。问A、B两地之间的距离是多少千米?
A.300
B.240
C.210
D.180
解析
第一步,本题考查行程问题,属于基本行程类。
第二步,设原来的速度为x千米/小时,则返程时前半段速度为(x-20)千米/小时,由早上8点从A地出发,11点到达B地,可知从A到B花费3小时,到达B地停留半小时,即11:30从B地出发,15点到达A地,则从B地到A地花费3.5小时,已知返回后半程速度变为之前的速度,说明返回后半程用时为1.5小时,那么返回前半程用时3.5-1.5=2(小时)。
第三步,由往返路程相等可列方程:3x=2(x-20)+1.5x,解得x=80,则A、B两地相距3×80=240(千米)。
因此,选择B选项。
4.(单选题)抛掷两颗质地均匀的骰子,记录向上的面出现的数字,那么这两个数字之和等于8的概率是:
A.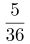
B.
C.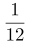
D.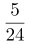
解析
第一步,本题考查概率问题,属于基本概率。
第二步,掷两颗质地均匀的骰子,满足向上的点数之和为8,可分为5种情况:(2,6)、(3,5)、(4,4)、(5,3)、(6,2)。总的情况数为6×6=36(种),故概率= =
=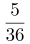 。
。
因此,选择A选项。
5.(单选题)10个相同的盒子中分别装有1—10个球,任意两个盒子中的球数都不相同,小李分三次,每次取出若干个盒子,每次取出的盒子中的球数之和都是上一次的3倍,且最后剩下一个盒子。剩下的盒子中有多少个球?
A.9
B.6
C.5
D.3
解析
第一步,本题考查其他杂题。
第二步,设第一次取出的球数之和为x,则第二次为3x,第三次为9x。最后剩下的盒子球数为y。
第三步,所有球的数字之和为1+2+3+4+5+6+7+8+9+10=55。则有x+3x+9x+y=55,化简为13x+y=55。
第四步,使用代入排除法,只有D项y=3代入,解得x=4,满足题意。
因此,选择D选项。
6.(单选题)几个朋友相约游泳,男士统一戴白色泳帽,女士统一戴红色泳帽。每位男士看到的白色泳帽数量与红色泳帽数量一样多,每位女士看到的白色泳帽数量都是红色泳帽数量的倍数。女士最少有( )人。
A.1
B.2
C.3
D.4
解析
第一步,本题考查基础应用题,用代入排除法解题。
第二步,根据每位男士看到的白色泳帽数量与红色泳帽数量一样多,得男士比女士多一人,设女士有x人,即男士有(x+1)人;设每位女士看到的白色泳帽数量为红色的n倍,得:(x+1)=n(x-1)。
第三步,题目求女士最少,选项由小到大依次代入:
A选项,当x=1时,x-1=0,n无解,排除;
B选项,当x=2时,解得n=3,符合题意。
因此,选择B选项。
7.(单选题)一个人工湖的湖面上有一个露出水面3米的圆锥体人工景观(底面朝下)。如人工湖水深减少20%,则该景观露出水面部分的体积将增加61/64。问原来的人工湖水深为多少米?
A.3.5
B.3.75
C.4.25
D.4.5
解析
第一步,本题考查几何问题,属于立体几何。
第二步,水深变化前后体积比为1:(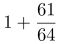 )=64:125,由于底面积不变,根据定理“立体图形中,体积之比等于相似比的立方”,则圆锥前后的高度之比为4:5,原来是3米,则水深减少之后是3÷
)=64:125,由于底面积不变,根据定理“立体图形中,体积之比等于相似比的立方”,则圆锥前后的高度之比为4:5,原来是3米,则水深减少之后是3÷ =3.75米。前后水深减少了0.75米是人工湖水深的20%,那么人工湖水深为0.75÷20%=3.75米。
=3.75米。前后水深减少了0.75米是人工湖水深的20%,那么人工湖水深为0.75÷20%=3.75米。
因此,选择B选项。
8.(单选题)一车救灾物资从早上8点起开始运往1900公里外的某地,白天平均车速80公里/小时,夜间60公里/小时(假定8:00到18:00为白天,其他时段为夜间),司机每驾驶2小时必须休息20分钟,且每名司机每天驾驶时间不能超过8小时(00:00后即为新的一天)。问车上至少应配备几名司机且至少要用多长时间才能抵达该地?
A.3名;27小时15分
B.3名;27小时25分
C.4名;33小时30分
D.4名;33小时40分
解析
第一步,本题考查统筹优化问题。
第二步,一天24小时,每名司机每天驾驶时间不超过8小时,故配备3名司机即可,3名司机可互相接替轮流驾驶,这样可以连续驾驶不用休息。8点—18点共10小时,可行驶80×10=800(公里);18点—第二天早上8点共14小时,可行驶60×14=840(公里),第二天8点时还差1900-800-840=260(公里),需要260÷80=3.25(小时)即3小时15分钟,那么共需要24小时+3小时15分钟=27小时15分钟。
因此,选择A选项。
9.(单选题)有A、B两种商品,如果A的利润增加20%,B的利润减少10%,那么A、B两商品的利润就相同了。问原来A商品的利润是B商品利润的百分之几?
A.80%
B.70%
C.85%
D.75%
解析
解法一:
第一步,本题考查经济利润问题,属于基础公式类,用方程法解题。
第二步,设A、B商品原来的利润为x、y。由A的利润增加20%可知,A的现利润为(1+20%)x;由B的利润减少10%可知,B的现利润为(1-10%)y。由利润相同,可得(1+20%)x=(1-10%)y,解得x∶y=75%。即原来A商品的利润是B的75%。
因此,选择D选项。
解法二:
第一步,本题考查经济利润问题,属于基础公式类,用赋值法解题。
第二步,赋值A商品原来的利润是100,那么增加20%后是120,等于B商品的现利润,则B商品原来的利润是120÷0.9=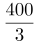 ,故原来A的利润是B的100∶
,故原来A的利润是B的100∶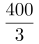 =75%。
=75%。
因此,选择D选项。
10.(单选题)某一天节秘书发现办公桌上的台历已经有9天没有翻了,就一次翻了9张,这9天的日期加起来的数恰好是108,问这一天是几号?
A.14
B.13
C.17
D.19
解析
第一步,本题考查星期日期问题
第二步,由选项可知这9天是连续的日期,构成公差为1的等差数列,根据9天日期加和等于108,可得中位数为108÷9=12,第5张为12号,因为等差数列的平均数等于中位数,所以第9张为12+(9-5)×1=16号,因此这一天为17号。
因此,选择C选项。
?
A.1年
B.2年
C.3年
D.4年
解析
第一步,本题考查星期日期问题。
第二步,若地球绕太阳公转的周期是365天8小时,普通的平年一年是365天的话,每三年会多出8×3=24小时,即一天,需要设置一个闰年。
因此,选择C选项。
2.(单选题)某新建高速公路中间隔离带绿化时,顺次种植2株蜀桧、3株刺柏、5株小叶女贞、3株大叶黄杨,按此循环,第2019株树木是什么?
A.蜀桧
B.刺柏
C.小叶女贞
D.大叶黄杨
解析
第一步,本题考查循环周期问题。
第二步,一个循环周期共有2+3+5+3=13(株)树木,2019÷13=155……4,可得155个周期后还剩余4株树,剩余的4株树木为2株蜀桧,2株刺柏,那么第2019株树木为刺柏。
因此,选择B选项。
3.(单选题)小许早上8:00从A地开车去B地取一批货物,他全程保持匀速并于11:00到达B地。在到达B地30分钟后,小许以比来时慢20千米/小时的速度驶回A地,并在行驶一半距离后恢复至原速度,并于15:00抵达A地。问A、B两地之间的距离是多少千米?
A.300
B.240
C.210
D.180
解析
第一步,本题考查行程问题,属于基本行程类。
第二步,设原来的速度为x千米/小时,则返程时前半段速度为(x-20)千米/小时,由早上8点从A地出发,11点到达B地,可知从A到B花费3小时,到达B地停留半小时,即11:30从B地出发,15点到达A地,则从B地到A地花费3.5小时,已知返回后半程速度变为之前的速度,说明返回后半程用时为1.5小时,那么返回前半程用时3.5-1.5=2(小时)。
第三步,由往返路程相等可列方程:3x=2(x-20)+1.5x,解得x=80,则A、B两地相距3×80=240(千米)。
因此,选择B选项。
4.(单选题)抛掷两颗质地均匀的骰子,记录向上的面出现的数字,那么这两个数字之和等于8的概率是:
A.
B.
C.
D.
解析
第一步,本题考查概率问题,属于基本概率。
第二步,掷两颗质地均匀的骰子,满足向上的点数之和为8,可分为5种情况:(2,6)、(3,5)、(4,4)、(5,3)、(6,2)。总的情况数为6×6=36(种),故概率=
 =
=因此,选择A选项。
5.(单选题)10个相同的盒子中分别装有1—10个球,任意两个盒子中的球数都不相同,小李分三次,每次取出若干个盒子,每次取出的盒子中的球数之和都是上一次的3倍,且最后剩下一个盒子。剩下的盒子中有多少个球?
A.9
B.6
C.5
D.3
解析
第一步,本题考查其他杂题。
第二步,设第一次取出的球数之和为x,则第二次为3x,第三次为9x。最后剩下的盒子球数为y。
第三步,所有球的数字之和为1+2+3+4+5+6+7+8+9+10=55。则有x+3x+9x+y=55,化简为13x+y=55。
第四步,使用代入排除法,只有D项y=3代入,解得x=4,满足题意。
因此,选择D选项。
6.(单选题)几个朋友相约游泳,男士统一戴白色泳帽,女士统一戴红色泳帽。每位男士看到的白色泳帽数量与红色泳帽数量一样多,每位女士看到的白色泳帽数量都是红色泳帽数量的倍数。女士最少有( )人。
A.1
B.2
C.3
D.4
解析
第一步,本题考查基础应用题,用代入排除法解题。
第二步,根据每位男士看到的白色泳帽数量与红色泳帽数量一样多,得男士比女士多一人,设女士有x人,即男士有(x+1)人;设每位女士看到的白色泳帽数量为红色的n倍,得:(x+1)=n(x-1)。
第三步,题目求女士最少,选项由小到大依次代入:
A选项,当x=1时,x-1=0,n无解,排除;
B选项,当x=2时,解得n=3,符合题意。
因此,选择B选项。
7.(单选题)一个人工湖的湖面上有一个露出水面3米的圆锥体人工景观(底面朝下)。如人工湖水深减少20%,则该景观露出水面部分的体积将增加61/64。问原来的人工湖水深为多少米?
A.3.5
B.3.75
C.4.25
D.4.5
解析
第一步,本题考查几何问题,属于立体几何。
第二步,水深变化前后体积比为1:(
因此,选择B选项。
8.(单选题)一车救灾物资从早上8点起开始运往1900公里外的某地,白天平均车速80公里/小时,夜间60公里/小时(假定8:00到18:00为白天,其他时段为夜间),司机每驾驶2小时必须休息20分钟,且每名司机每天驾驶时间不能超过8小时(00:00后即为新的一天)。问车上至少应配备几名司机且至少要用多长时间才能抵达该地?
A.3名;27小时15分
B.3名;27小时25分
C.4名;33小时30分
D.4名;33小时40分
解析
第一步,本题考查统筹优化问题。
第二步,一天24小时,每名司机每天驾驶时间不超过8小时,故配备3名司机即可,3名司机可互相接替轮流驾驶,这样可以连续驾驶不用休息。8点—18点共10小时,可行驶80×10=800(公里);18点—第二天早上8点共14小时,可行驶60×14=840(公里),第二天8点时还差1900-800-840=260(公里),需要260÷80=3.25(小时)即3小时15分钟,那么共需要24小时+3小时15分钟=27小时15分钟。
因此,选择A选项。
9.(单选题)有A、B两种商品,如果A的利润增加20%,B的利润减少10%,那么A、B两商品的利润就相同了。问原来A商品的利润是B商品利润的百分之几?
A.80%
B.70%
C.85%
D.75%
解析
解法一:
第一步,本题考查经济利润问题,属于基础公式类,用方程法解题。
第二步,设A、B商品原来的利润为x、y。由A的利润增加20%可知,A的现利润为(1+20%)x;由B的利润减少10%可知,B的现利润为(1-10%)y。由利润相同,可得(1+20%)x=(1-10%)y,解得x∶y=75%。即原来A商品的利润是B的75%。
因此,选择D选项。
解法二:
第一步,本题考查经济利润问题,属于基础公式类,用赋值法解题。
第二步,赋值A商品原来的利润是100,那么增加20%后是120,等于B商品的现利润,则B商品原来的利润是120÷0.9=
因此,选择D选项。
10.(单选题)某一天节秘书发现办公桌上的台历已经有9天没有翻了,就一次翻了9张,这9天的日期加起来的数恰好是108,问这一天是几号?
A.14
B.13
C.17
D.19
解析
第一步,本题考查星期日期问题
第二步,由选项可知这9天是连续的日期,构成公差为1的等差数列,根据9天日期加和等于108,可得中位数为108÷9=12,第5张为12号,因为等差数列的平均数等于中位数,所以第9张为12+(9-5)×1=16号,因此这一天为17号。
因此,选择C选项。
?










