在具体工作中,自然科学专业技术人员常常要和各种数据打交道,并且要对数据具有一定的敏感性。能对数据真伪进行识别,能对数据进行有效的分析、转化、应用,这是自然科学专业技术人员必须具备的能力。本文将讲解科技实务题-计算类,计算类的解题关键在于了解加权平均数的概念。
算术平均数是平均数中最基本也是最常用的形式,也是为大众最熟知的。它是总体单位的某种标志数值的总和除以与之相适应的单位总数所求得的商。
类型一:简单算术平均数:资料中未分组时可以采用简单算术平均数的方法
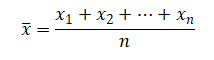
其中,x为变量值,n为变量值的个数。
类型二:加权算术平均数:与简单算术平均数不同,它不像简单平均数一样只受一个因素的影响,即变量值的影响,它还受到权数的影响。在平均数计算中,区别各个标志值相对重要性的计量数值,称之为权数,又称权重。
加权算术平均数通常是在分组资料,各个变量值出现的次数不等的情况下使用,公式如下:
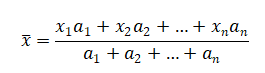
其中,x为各组变量值或组中值,a为各组的权重。
【例1】张学生参加某次事业单位公考,总成绩由4部分组成,分别为职测部分、综合部分、面试、体测,每部分满分为100分。职测部分分数按30%计算,综合部分分数按40%计算,面试按20%计算,体测按10%计算。某考生职测分数78分,综合分数85,面试分数82分,体测分数89分,问该考生总成绩为多少?
【图图解析】

要去计算考生总成绩为多少就要把分数×占比,计算加权算术平均数。

【例2】下面是某研究人员绘制的关于我国城乡基本公共服务均等化水平评价研究的两个表。表1是此项评价研究的指标体系及权重,表2是全国各地区在3项指标(医疗卫生、基础设施、基本公共服务)上的均等化差异值及三者的综合均等化差异值。请根据这两张表回答问题。
表1城乡基本公共服务均等化评价指标体系及权重
| 一级指标 | 二级指标 | 三级指标 | ||
| 指标内容及代码 | 指标内容及代码 | 权重 | 指标内容及代码 | 权重 |
| 城乡基本公共服务综合指数 (A) | 医疗卫生 (B1) | 0.409 | 每千人卫生技术人员数(人)(C1) | 0.273 |
| 每千人执业医师数(人)(C2) | 0.409 | |||
| 每千人医疗卫生机构床位数(张)(C3) | 0.318 | |||
| 基础设施 (B2) | 0.273 | 供水普及率(%)(C4) | 0.316 | |
| 燃气普及率(%)(C5) | 0.263 | |||
| 人均道路面积(平方米)(C6) | 0.421 | |||
| 基础公共教育 (B3) | 0.318 | 大专及以上人口占比(%)(C7) | 0.226 | |
| 高中文化人口占比(%)(C8) | 0.290 | |||
| 初中文化人口占比(%)(C9) | 0.258 | |||
| 小学文化人口占比(%)(C10) | 0.129 | |||
| 未上过小学人口占比(%)(C11) | 0.097 | |||
表2全国各地区城乡各分项指标的均等化差异值及综合均等化差异值
| 地区代码 | 医疗卫生 | 基础设施 | 基本公共教育 | 综合均等化差异 | 经济发展水平排名 | 地区代码 | 医疗卫生 | 基础设施 | 基本公共教育 | 综合均等化差异 | 经济发展水平排名 |
| D1 | 0.600 | 0.375 | 0.576 | 0.531 | 13 | D16 | 0.542 | 0.599 | 0.341 | 0.494 | 5 |
| D2 | 0.214 | 0.588 | 0.684 | 0.466 | 20 | D17 | 0.355 | 0.635 | 0.481 | 0.672 | 9 |
| D3 | 0.642 | 0.750 | 0.262 | 0.551 | 6 | D18 | 0.527 | 0.700 | 0.246 | 0.485 | 10 |
| D4 | 0.617 | 0.567 | 0.537 | 0.578 | 21 | D19 | 0.723 | 0.434 | 0.498 | 0.573 | 1 |
| D5 | 0.681 | 0.822 | 0.436 | 0.642 | 15 | D20 | 0.319 | 0.515 | 0.272 | 0.358 | 18 |
| D6 | 0.279 | 0.672 | 0.696 | 0.519 | 7 | D21 | 0.474 | 0.341 | 0.449 | 0.430 | 28 |
| D7 | 1.000 | 0.666 | 0.565 | 0.770 | 22 | D22 | 0.052 | 0.529 | 0.463 | 0.313 | 23 |
| D8 | 0.453 | 0.427 | 0.580 | 0.486 | 17 | D23 | 0.323 | 0.640 | 0.317 | 0.408 | 8 |
| D9 | 0.170 | 0.100 | 0.578 | 0.281 | 11 | D24 | 0.408 | 0.499 | 0.441 | 0.443 | 26 |
| D10 | 0.409 | 0.455 | 0.477 | 0.443 | 2 | D25 | 0.615 | 0.790 | 0.405 | 0.596 | 24 |
| D11 | 0.387 | 0.559 | 0.428 | 0.447 | 4 | D26 | 0.379 | 0.719 | 0.286 | 0.442 | 16 |
| D12 | 0.299 | 0.697 | 0.352 | 0.425 | 14 | D27 | 0.312 | 0.675 | 0.405 | 0.441 | 27 |
| D13 | 0.542 | 0.423 | 0.444 | 0.478 | 12 | D28 | 0.525 | 0.637 | 0.492 | 0.545 | 29 |
| D14 | 0.437 | 0.640 | 0.291 | 0.446 | 19 | D29 | 0.647 | 0.478 | 0.711 | 0.621 | 25 |
| D15 | 0.334 | 0.666 | 0.413 | 0.450 | 3 | 均值 | 0.457 | 0.569 | 0.453 | 0.486 | ? |
研究人员在录入表2的数据时,不慎将其中一个地区的“综合均等化差异”值录入错误,请在答题卡的横线处写出该地区的代码,并计算其正确数值(四舍五入保留三位小数)。
【图图解析】
因为表格的内容发现和表一的权重有关系,综合均等化差异值是前面三个值的加权平均数,总体值为每个部分值之间,根据综合均等化差异值和医疗卫生值、基础设施值和基本公共教育值之间的关系,可以观察出数据的不准确性,发现D17值有误,D17的值太大,正确计算为0.355×0.409+0.635×0.273+0.481×0.318=0.145195+0.173355+0.152958=0.471508≈0.472。










