题型：单选题（分值：1）

　　有一高12厘米的棱柱，其底面为边长6厘米的正六边形，现在棱柱底部挖出一个半球，问剩余体积最小为多少立方厘米？

　　A.216－27π

　　B.21654π

　　C.64827π

　　D.64854π

　　答案：D

　　解析：

　　第一步，本题考查几何问题。

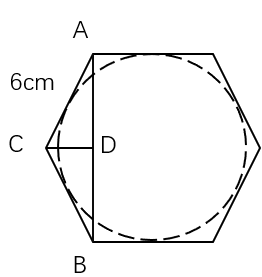
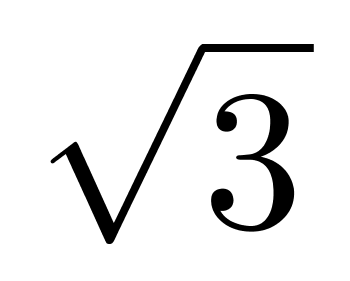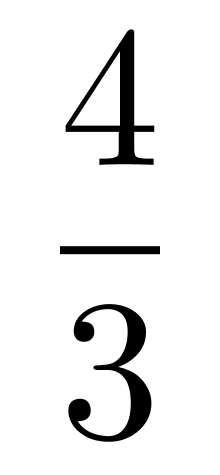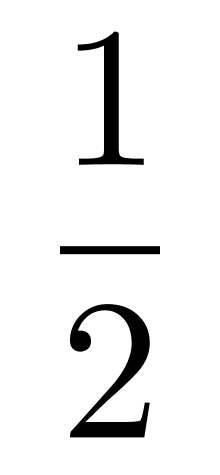　　第二步，要使剩余体积最小，则挖出的半球体积要尽可能大，根据题意可得下图，当半球的底面为正六边形的内接圆时，半球体积最大。连接A、B，底面圆的直径与AB等长，根据题意可知，∠CAD＝30°，∠ADC＝90°，AC＝6厘米，可得AD＝6×＝3厘米，即圆的半径为3厘米，因此半球体积为：×π×（3）?×＝54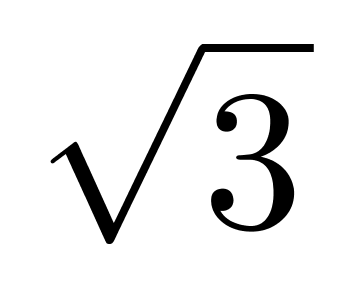π立方厘米。棱柱底面可看作6个全等的正三角形，边长为6厘米，每个正三角形的面积为×6×3＝9平方厘米，可得棱柱底面积为6×9＝54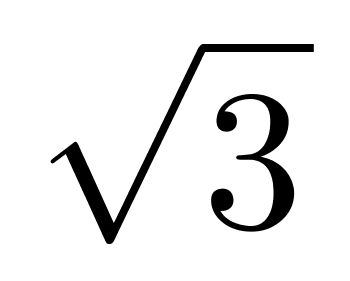平方厘米，棱柱体积为54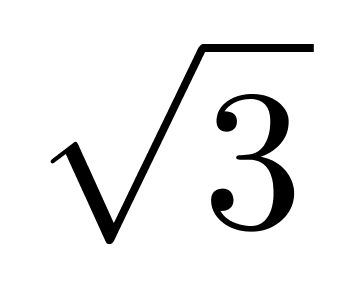×12＝648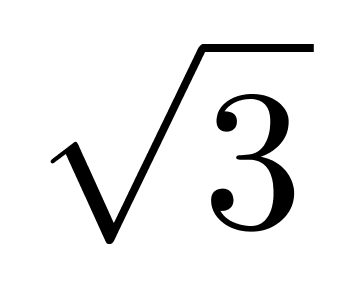立方厘米，故剩余体积最小为648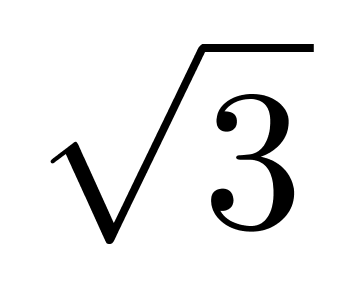－54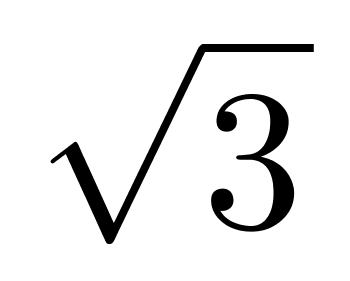π立方厘米。

　　因此，选择D选项。

　　来源：2025年安徽省公务员考试模考(第一期)

　　以上是安徽省公务员模考的试卷的部分试题内容，更多2025年安徽公务员考试,安徽省考模考,安徽公务员模考，请继续查看2025年安徽省公务员考试模考(第一期)试题题库或最新公务员试题题库。