1.题目:九年级《蒙古包圆柱圆锥侧面积》片段教学
2.内容:

3.基本要求:
(1)试讲约10分钟;
(2)有分析、解决问题的过程;
(3)要有讨论环节,
(4)要有适当板书。
【试题解析】
一、创设情境,悬疑导入
问题1:同学能举出生活中见到的圆柱、圆锥吗?我们能计算这些物体的那些量呢?
把问题重点放在侧面积的计算上。
回顾复习:圆柱、圆锥侧面积计算的思路以及公式。
问题2:生活中有这么多的圆柱、圆锥、必然在生活会有关于它们的数学计算,今天,我们一起来走进关于圆柱和圆锥侧面积的应用。引出课题《蒙古包圆柱圆锥侧面积》。
二、合作探究,新课讲授
(一)呈现情境,提出问题
创设蒙古包的情境问题,PPT呈现直观图片。

提出问题1:这个问题的突破口在哪里?
诱导学生思考明确:求出一个蒙古包需要用的毛毡的面积。
问题2:那么,一个蒙古包需要用的毛毡的面积该怎么计算呢?
引导学生小组讨论,思考解决方案
(二)画示意图,明确思路
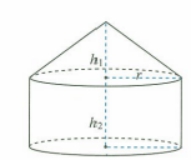
把实际问题抽象成数学问题。ppt呈现几何直观图。
问题1:我们要求是圆柱和圆柱的那些面积呢?
明确:求圆锥和圆柱的侧面积。不需要求底面积,点出易错点。
问题2:我们已知哪些数学量,会利用哪些公式求解呢?
明确:先要利用圆的面积公式求出底面圆的半径,使用圆柱和圆锥的侧面积公式求一个蒙古包的侧面积。
(三)完成解题
问题:那么大家会计算了吗,给大家5分钟时间,大家自主或合作完成,待会请代表上台板演?
学生自主完成解题。

思考:大家求出结果了吗?这个结果就是我们问题所求吗?
点出易错点:容易忘记实际问题是要求20个蒙古包所需要的毛毡面积。
![]()
问题:大家可以总结一下在解决实际问题时的一般思路吗?
明确步骤:①审题,明确题意和所求;②把实际问题抽象为数学问题;③思考确定解题思路;④动手实践完善解题过程,发现解决过程的易错点;⑤检验结果,解决问题。
三、巩固应用,内化提高
1.ppt呈现应用题,引导学生以小组为单位解决问题,以小组pk的形式,提高解决问题的热情,对于学生积极表现给予肯定评价。不仅要重结果,更加需要注重学生过程的点播。

(要求学生说明理由。)
四、回顾整理,反思提升
通过今天的实际应用,大家有哪些收获呢,可以说一说,知识上的,方法上的,数学思想上的,等等都行。
引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识的归纳,纳入自己的知识结构。
总结解决问题的一般步骤:①审题,明确题意和所求;②把实际问题抽象为数学问题;③思考确定解题思路;④动手实践完善解题过程,发现解决过程的易错点;⑤检验结果,解决问题。
五、知识拓展,布置作业
1.完成课后习题1题;
2.思考生活中圆柱、圆锥侧面积的应用,下节课一起展示分享。
板书设计:
蒙古包圆柱圆锥侧面积
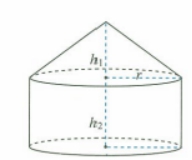
解题思路:①求底面半径r,②求圆柱侧面积,③求圆锥母线长;
④圆锥底面周长;⑤求圆锥侧面积;⑥求出所求。
总结:
①审题,明确题意和所求;
②把实际问题抽象为数学问题;
③思考确定解题思路;
④动手实践完善解题过程,发现解决过程的易错点;
⑤检验结果,解决问题。
1.题目:九年级《直线和圆的位置关系》片段教学
2.内容:
3.基本要求:
(1)试讲约10分钟;
(2)需要师生互动环节;
(3)要有适当板书。
【试题解析】
一、情境导入

先复习点和圆的三种位置关系及圆心到点的距离d与半径r的关系由此引出本节课直线与圆的位置关系。?
观察一轮红日从海平面升起的三幅照片,提出问题:
师:请仔细观察“日出”的运动过程,描绘出其运动轨迹是怎样的几何图形?
请同学们猜想并动手画一画。能不能结合我们学过的知识,把它们抽象出几何图形,总结出直线和圆有几种位置关系??
二、探究新知
师:下面老师先画一个圆。?
师:我们把直尺的边缘看作一条直线,任意移动直尺。同学们想一想,这一过程中直线和圆的公共点可能有多少个??
生:直线和圆公共点可能有0个,1个,2个。
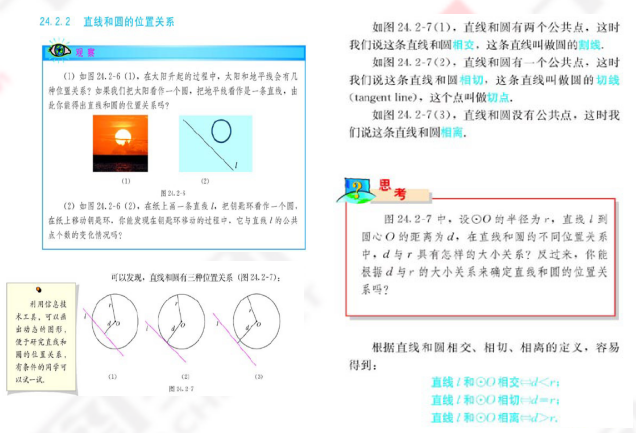
师:根据公共点的个数,我们把直线和圆位置关系分成三种,即没有公共点叫相离,唯一公共点叫相切,两个公共点叫相交。
师:我们知道要判断点和圆的位置关系可以根据点到圆心的距离与半径的大小来判断,那么要判断直线和圆的位置关系可不可以用类似的方法呢?下面请一位同学画出圆心到直线的距离d??
师:看图形你发现了什么??
生:我发现了直线与圆相离时,d>r;相切时,d=r;相交时,d
师:这是已知了直线与圆的位置关系,得出对应的数量关系,反过来,如果已知数量关系,可不可以得出对应的位置关系呢?用这种数量关系来判断直线与圆的位置关系,关键是要知道d和r,然后比较d与r大小,从而确定位置关系。
三、巩固练习
在码头A的北偏东60方向有一个海岛,离该岛中心P的15海里范围内是一个暗礁区。 货船从码头A由西向东方向航行,行驶了1 8海里到达B,这时岛中心P在北偏东30方向。若货船不改变航向,问货船会不会进入暗礁区?
让学生完整解答。
四、归纳小结
今天你有哪些收获?师生共同总结。
五、布置作业
寻找身边有哪些设计体现了直线与圆的位置关系。
板书设计:
直线与圆的位置关系
相离:d>r;
相切:d = r;
相交:d <r
1.题目:八年级《待定系数法求一次函数》片段教学
2.内容:

3基本要求:
(1)试讲约10分钟;
(2)讲解待定系数法的解题步骤;
(2)要有讨论环节,
(4)要有适当板书。
【试题解析】
一、回顾复习,谈话导入
教师在黑板上画出一次函数的四种类型的图象,要学生判断k和b的符号。
提问:试画出y=x+3的图象,能准确判断出k和b的符号吗?
预设学生行为:能准确判断出k和b的符号,大部分同学能画出一次函数的图象。
提问:我们知道一次函数的图象是一条直线,而两点确定一条直线,那么,如果我们知道一次函数经过的两个点的坐标,能求出这一个一次函数吗?
引出课题“用待定系数法求一次函数”(板书课题)。
二、合作探究,新课讲授
(一)分析、解决问题
提出问题:给出一个一次函数的图象,如何求出函数图象的解析式,学生思考。
预设学生行为:学生可能会想到找两个点,求出k和b就可以
用ppt呈现跟课题相关的数学问题。以教材例4为主。

题目1:命题(分清题设与结论)改成如果那么的形式

最后,华图教师希望各位考生能够努力学习、积极备考、持之以恒、克服困难,早日圆教师梦想!
文章来源于中国教师资格网











