题型:单选题(分值:1)
83 、某次抽奖活动在三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖,摸出的3个球中至少有一个绿球的得二等奖,摸出的3个球均为彩色球(黑、白除外)的得三等奖。问不中奖的概率是多少?
A.在0—25%之间
B.在25—50%之间
C.在50—75%之间
D.在75—100%之间
答案:B
解析:解法一:
第一步,本题考查概率问题,属于分类分步型。
第二步,均为彩色球的情况包含了均为红球的情况(无黑、白、绿球),故得一等奖和三等奖共有5?=125(种)方法。至少有一个绿球的反面情况是没有绿球,故得二等奖有8?-7?=169(种)。
第三步,中奖共有125+169=294(种),摸3个球的总方法数有8?=512(种),故不中奖的概率为1-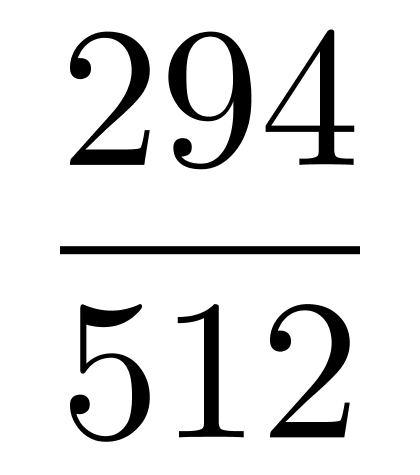 ≈42%。
≈42%。
因此,选择B选项。
解法二:
第一步,本题考查概率问题,属于分类分步型。
第二步,若抽到的3个球中有黑、白球且无绿球则不中奖,分三种情况讨论:
(1)3个球都是黑、白球,概率为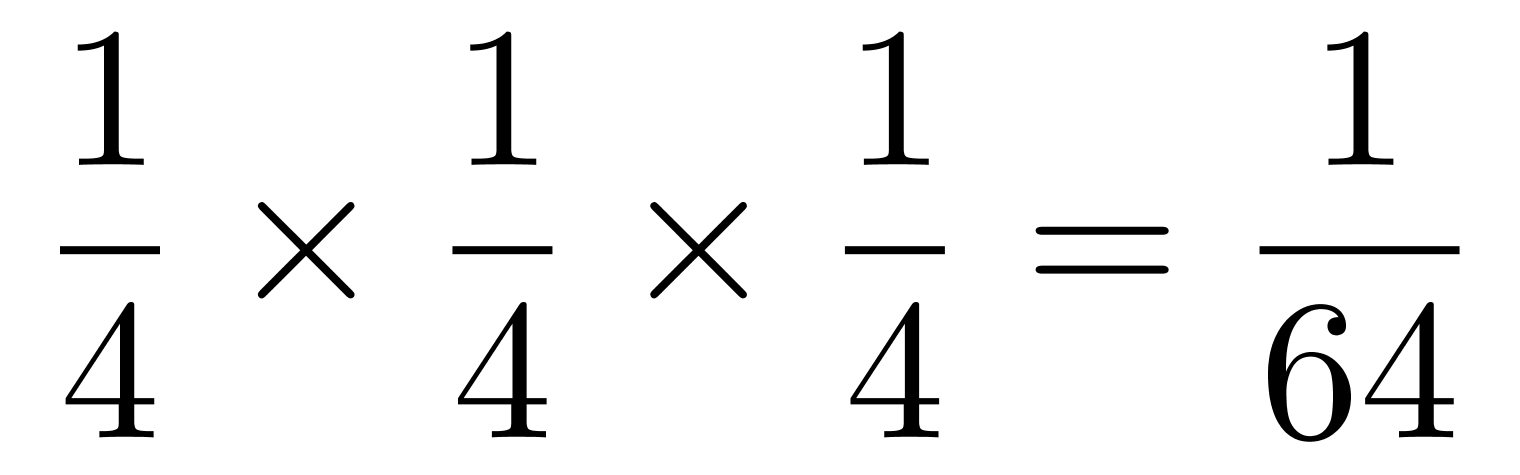 ;
;
(2)3个球有2个是黑、白球,1个是其他球(非黑、白、绿),概率为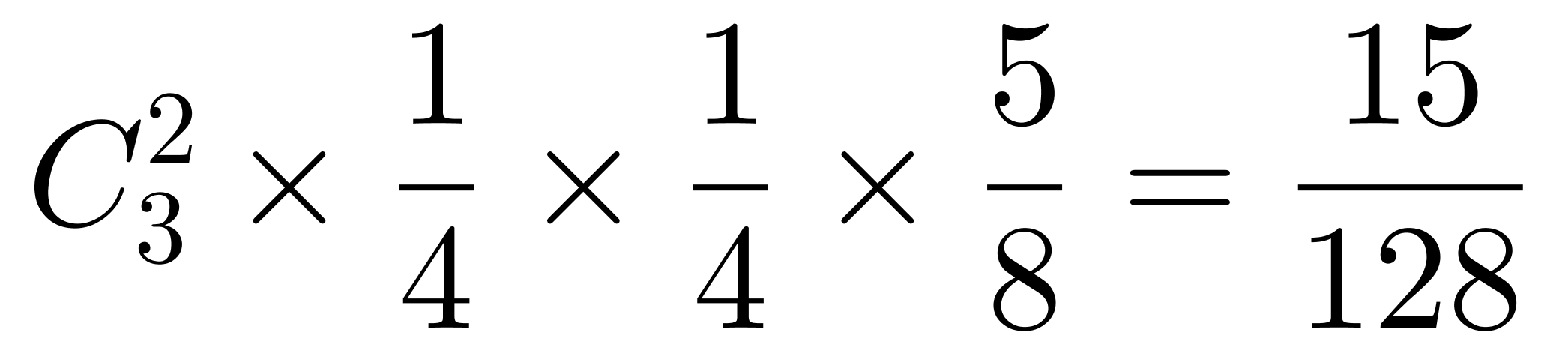 ;
;
(3)3个球有1个是黑、白球,2个是其他球(非黑、白、绿),概率为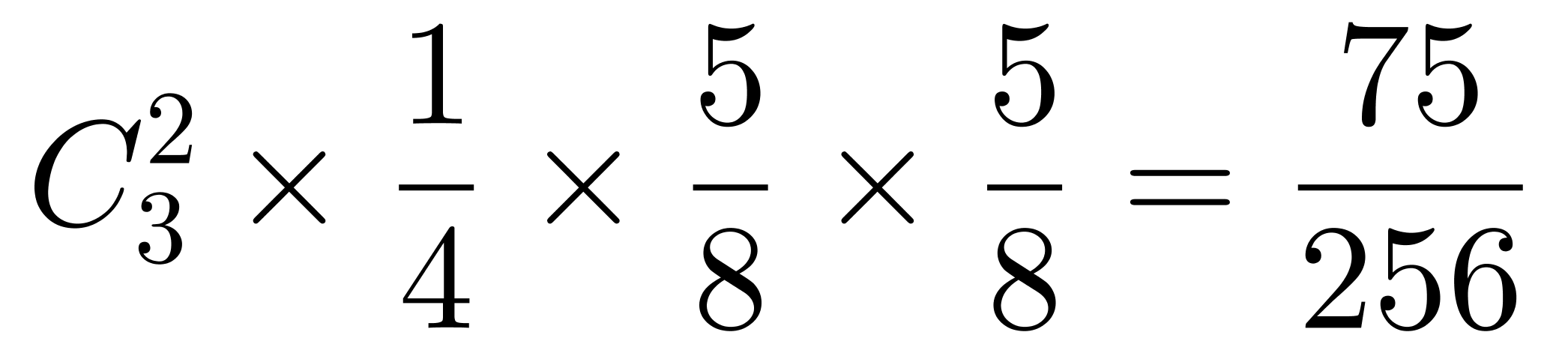 ;
;
则不中奖的概率为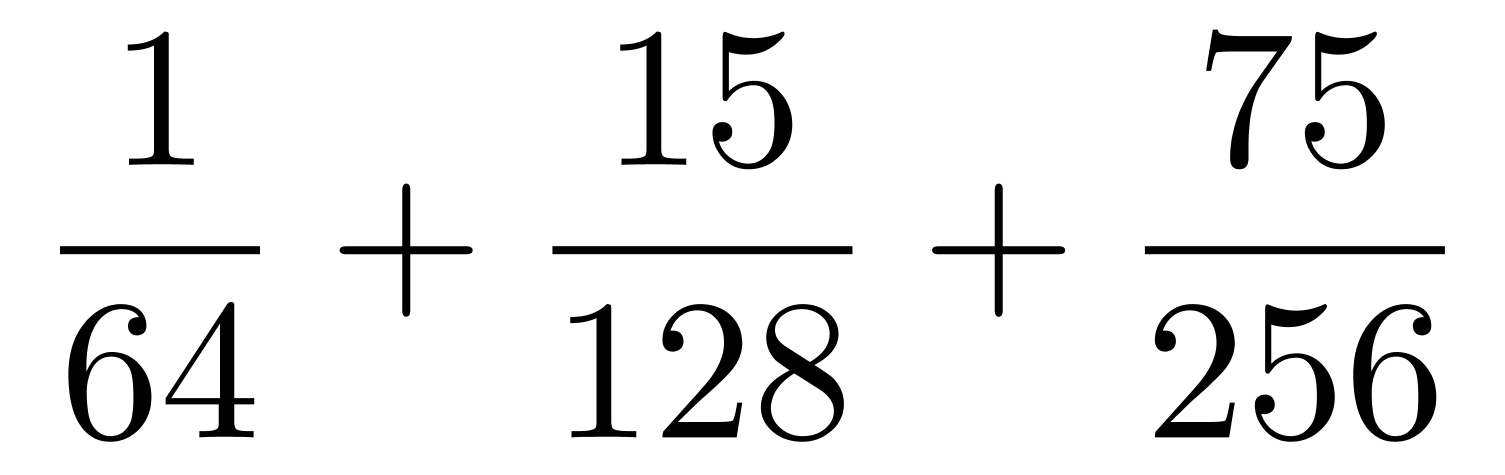 ≈42%。
≈42%。
因此,选择B选项。
要点:数量关系 ?数学运算 ?概率问题 分类分步型 ?
以上是2013年0413黑龙江公务员考试题的试卷的部分试题内容,更多黑龙江公务员考试试题,黑龙江省考试题答案,黑龙江公务员行测答案,请继续查看2013年0413黑龙江公务员考试《行测》试题试题题库或最新公务员试题题库。











