平面几何—将军饮马（最短路径）

　　“将军饮马”是我国最古老的数学题型之一。

　　唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河。”大致的意思是：“白天登山观察报警的烽火台，黄昏时牵马饮水靠近交河边。”在这两句诗终隐含这一个有趣的数学问题：黄昏时将军从烽火台到交河饮马后回军营休息，怎样走才能使路程最短呢？

　　其实解决这个问题并不难，先将其抽象为数学模型：直线l同侧有两个定点A、B，在直线l上找一点C使AC+BC最小即可（如下图）。

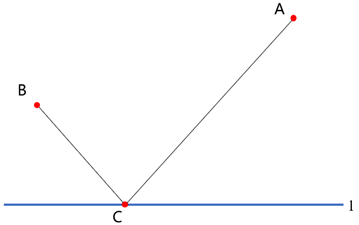
　　说到两点之间最短距离我们一定会想到点到点最值模型：“两点之间线段最短”，但是，A、B两点在直线l的同侧，直接连接AB并不会交于直线l。所以我们解决此类题型可以假定A、B两点在直线l的两侧，则可连接AB交直线l于点C。因此，我们可以找点A关于直线l的对称点，再连接A’B交直线l于点C，点C即为所求！

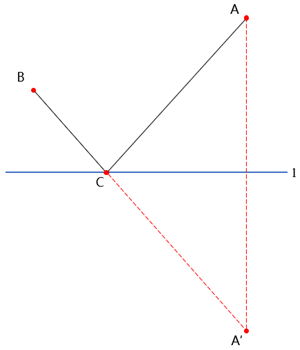
　　下列我们来看两道例题，实操一下。

　　【例1】 悟空与二郎神在离地面1米的空中决斗，两人相距2米，悟空想用分身直接偷袭二郎神，为了不引起对方的警觉，分身必须在地面反弹一次再进行攻击，则分身到达二郎神的位置所走的最短距离为：

　　【答案】A

　　【解析】第一步，本题考查几何问题，属于其他几何类。

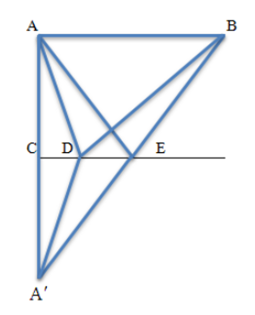
　　第二步，如图所示，假设A为悟空所在位置，A'为其相对地面的对称点，B为二郎神的位置。分身必须在地面反弹一次，分身到达二郎神的位置所走的路线有多种，如折线ADB所示。要使折线长度最短，则反弹点应位于A'B与地平线的交点E，AA'＝2米，则最短距离为AE＋EB＝A'E＋EB＝A'B＝（米）。

　　因此，选择A选项。

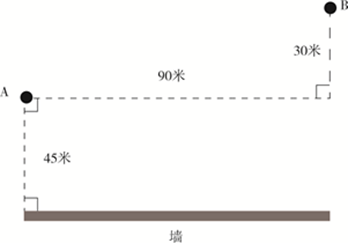
　　【例2】 A点、B点与墙的位置如右图所示，现从A点出发以5米/秒的速度跑向墙，接触到墙后再跑到B点，问最少要多少秒到达B点？

　　A. 30 B. 34

　　C. 38 D. 42

　　【答案】A

　　【解析】第一步，本题考查几何问题，属于平面几何类。

　　第二步，如图所示，作B点对称于墙为B'点，连接A、B'点，交墙于C点，作AD⊥D B'，在直角三角形ADB'中，AD=45＋30＋45=120（米），DB'＝90（米），则根据勾股定理得AB'=150（米）。

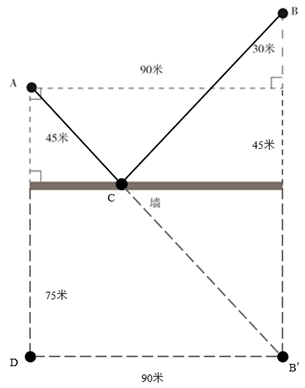
　　第三步，最短距离AC＋CB＝AB'=150（米），至少需要150÷5＝30（秒）。

　　因此，选择A选项。