【答案及解析】

　　1.【答案】C

　　【解析】第一步，本题考查排列组合问题，属于基础公式类。

　　2.【答案】B

　　【解析】第一步，本题考查排列组合问题，属于基础排列组合。

　　第二步，由平均分成两组知，第一组先选出5人有＝252（种）种分法，剩下5人自动成为第二组。 由于没有先后顺序区别，所以有 ＝126（种）。

　　因此，选择B选项。

　　3.【答案】A

　　【解析】第一步，本题考查排列组合问题。

　　第二步，在九盏灯中任取三盏，共有＝84（种）情况。但在同一直线上的三个点是不能构成三角形的，排除 8 种“三点一线 ”情况（如图），故可组成的三角形有 84－8 ＝76（种）。

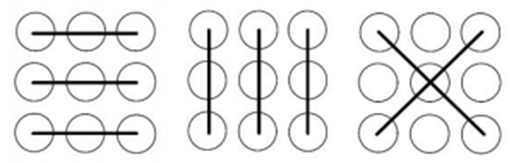
　　第三步，至少需要的时间为 76×3 ＝228（秒）。

　　因此，选择 A 选项。

　　4.【答案】D

　　【解析】第一步，本题考查排列组合问题，属于方法技巧型类。

　　第二步，此题要求每位玩家不能从贴有自己对应标签的迷宫出口出迷宫，也就是完全错位，属于错位排列问题，已知一共5个人，则5的错位排列数为44。

　　因此，选择D选项。

　　【拓展】错位排列数（Dn为n个元素的错位排列数）：D1 ＝0 ，D2 ＝1 ，D3 ＝2 ，D4 ＝9，D5 ＝44 ，D6 ＝265。

　　5.【答案】B

　　【解析】第一步，本题考查排列组合问题，属于方法技巧型类。

　　第二步，此题要求四个玩偶放到三个箱子中，不许有空箱子，则三个箱子分别装玩偶2、 1 、1。又因为任意一个玩偶都不能放入标有相同标号的箱子中，也就是标号1到3的玩偶放入箱子要考虑错位，分情况讨论：①先将标号1到3的玩偶分别放在三个箱子中，错位排列问题，3个物体错位排列数为2种；再把4号玩偶放入一个箱子中，情况数有 ＝3种，分两步总情况数＝2×3 ＝6种；②先将1到3号玩偶中的两个玩偶放在另一个编号一个箱子中，3种情况：1、2号玩偶放在3号箱子中，1 、3号玩偶放在2号箱子中，2 、3号玩偶放在1号箱子中；再把剩下的两个玩偶分别放到剩下的两个箱子中，情况数有 ＝2种，分两步总情况数＝3×2 ＝6种。

　　第三步，最终的方法①+② =6＋6 ＝12种。

　　因此，选择B选项。

　　【拓展】错位排列数（Dn意为n个元素的错位排列数）：D1 ＝0，D2 ＝1，D3 ＝2，D4 ＝9，D5 ＝44 ，D6 ＝265。