【答案及解析】

　　1.【答案】B

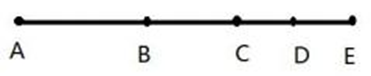
　　【解析】第一步，本题考查几何问题。

　　第二步，根据题意，AE 间所有可能的区段有 AB、AC 、AD 、AE 、BC 、BD 、BE 、CD 、CE 、DE，由 AE 间所有可能区段的长度之和为 96 ，则 AB＋AC＋AD＋AE＋BC＋BD＋BE＋CD+CE＋DE ＝4AE＋2BD ＝96 ，化简得 2AE＋BD ＝48。

　　第三步，代入 A 选项，若 AE ＝17，则 BD ＝14，那么 AB＋DE ＝3，不符合题意排除（AB 大于 BC 大于 CD 大于 DE）；代入 B 选项，若 AE ＝19 ，则 BD ＝10 ，那么 AB＋DE ＝9，AB=7 ，BC ＝6 ，CD ＝4 ，DE ＝2 ，这一组数满足题目所有条件。

　　因此，选择 B 选项。

　　2.【答案】C

　　【解析】第一步，本题考查几何问题，属于平面几何类。

　　第二步，设该半圆的半径为r厘米，则该半圆的面积＝＝1.57r2 ，根据题意： 15×12－1.57r2 ＝123.48 ，解得r ＝6（厘米）。

　　第三步，该半圆的周长＝圆周长的一半＋直径＝1/2 ×2πr＋2r ＝3. 14×6＋2×6 ＝30.84（厘米）

　　因此，选择C选项。

　　3.【答案】B

　　【解析】第一步，本题考查几何问题，属于立体几何类。

　　第二步，根据长方体体积公式＝长×宽×高，得内装水的体积＝6×6×8 ＝288（cm3），由于水的体积不会发生变化。

　　第三步，设放倒后容器内水面的高度为h，则放倒后内装水的体积＝6×12×h ＝288，解得h ＝4（cm ）。

　　因此，选择B选项。

　　4.【答案】C

　　【解析】第一步，本题考查几何问题。

　　第二步 ，设大圆直径为 D ， 小圆直径为D1 ，D2 ，D3……Dn- 1 ，Dn 。根据题干可知 D=D1+D2+D3+ …+Dn- 1+Dn 。 大 圆 周 长 为 πD ， 小 圆 周 长 和 为 πD1+πD2+πD3+…+πDn-1+πDn= π D 1+D2+D3+…+Dn-1+Dn) = πD。

　　因此，选择 C 选项。

　　5.【答案】C

　　【解析】第一步，本题考查几何问题，属于平面几何问题。

　　第二步，如右图所示，

　　四个同样大小的等腰直角三角形拼成一个正方形，每个三角形的面积为 9 平方厘米，则 正方形面积为 36 平方厘米，那么正方形的边长为 6 厘米，所以该正方形的周长为 6×4=24 （厘米）。

　　因此，选择 C 选项。