1.(单选题)某会展中心布置会场,从花卉市场购买郁金香、月季花、牡丹花三种花卉各20盆,每盆均用纸箱打包好装车运送至会展中心,再由工人搬运至布展区。问至少要搬出多少盆花卉才能保证搬出的鲜花中一定有郁金香?
A.20盆
B.21盆
C.40盆
D.41盆
解析
第一步,本题考查最值问题,属于最不利构造。
第二步,根据“至少……保证……”可知本题为最不利构造,答案为“所有最不利情况+1”。要求搬出的鲜花中一定有郁金香,最不利的情况是把所有月季花、牡丹花都搬出来,即搬出20+20=40(盆)。在此基础上再搬1盆,就能够保证搬出的鲜花中一定有郁金香,即至少要搬出40+1=41(盆)。
因此,选择D选项。
2.(单选题)某超市设有10个人工收银台。周末10个收银台全开,顾客结账平均排队20分钟。为提高效率,超市撤了4个人工收银台,并改造为6个自助收银台。若自助收银的效率是人工收银效率的90%。改造后,周末当人工收银台和自助收银台全开,预计顾客结账平均排队耗时约为?。
A.12分钟
B.14分钟
C.16分钟
D.18分钟
解析
第一步,本题考查工程问题效率类。
第二步,赋值每个人工收银台每分钟结账人数为1,那么总量= 。
。
每个自助收银台每分钟结账人数为0.9,那么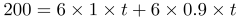 ,解得t=17.54分钟,取18分钟。
,解得t=17.54分钟,取18分钟。
因此,选择D选项。
3.(单选题)甲租用乙的地种粮食,今年共收获3000斤粮食,包括大米、玉米和红薯。其中玉米800斤,红薯600斤。如果除租金之外,甲每年须将收获的大米的N%给乙作为回报,同时将红薯超过粮食总重的15%的部分也按照N%给乙作为回报,甲今年一共给乙210斤粮食,那么N%为多少?
A.8%
B.12%
C.14%
D.16%
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,根据共收获3000斤粮食,可得大米产量为3000-800-600=1600(斤),则甲每年给乙的大米为1600×N%。又根据红薯超过粮食总重的15%部分为600-3000×15%=150(斤),则甲每年给乙的红薯为150×N%。
第三步,根据共给乙210斤粮食,可列方程1600×N%+150×N%=210,解得N%=12%。
因此,选择B选项。
4.(单选题)一辆车从甲地行驶到乙地共20千米,用时20分钟,已知该车在匀加速到最大速度后开始匀减速,到乙地时速度恰好为0,问该车行驶的最大速度是多少千米/小时?
A.100
B.108
C.116
D.120
解析
第一步,本题考查基本行程类。
第二步,根据均加(减)速运动中, ,设最大速度为v,则
,设最大速度为v,则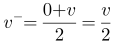 ,20分钟=
,20分钟=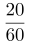 小时=
小时=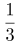 小时,根据s=
小时,根据s=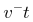 可得,20=
可得,20= ,解得v=120。
,解得v=120。
因此,选择D选项。
5.(单选题)甲、乙两个仓库共存有340吨粮食。如果甲仓库存放的粮食是乙仓库的2倍多10吨,则甲仓库存有粮食( )吨。
A.110
B.120
C.230
D.240
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,设乙仓库粮食为x吨,则甲仓库粮食为2x+10吨。
第三步,根据题干甲、乙两个仓库共存有340吨粮食,列出等量关系:x+2x+10=340,求出x=110,则甲为230吨。
因此,选择C选项。
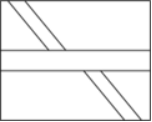
6.(单选题)如图所示,某地计划修建一个长50米、宽40米的长方形观光园。现在需要在观光园中修建几条鹅卵石小道供游客行走,其中一条是长为50米、宽为2米的水平直线型小路,另外两条修成斜线型,并且要求这两条斜线型小路任何地方的水平方向宽度都是1米,问修完小路后观光园剩下部分的面积是多少平方米?
A.1862
B.1880
C.1950
D.1960
解析
第一步,本题考查几何问题,属于平面几何类。
第二步,根据题意整个长方形观光园面积=50×40=2000(平方米)。其中水平直线型的小路面积=50×2=100(平方米),两条斜线型小路经过拼接可组合成一条底为1,高为38的平行四边形小路,面积=1×38=38(平方米)。
第三步,修完小路后观光园剩下部分的面积=2000-100-38=1862(平方米)。
因此,选择A选项。
7.(单选题)某企业年终评选了30名优秀员工,分三个等级,分别按每人10万元、5万元、1万元给与奖励。若共发放奖金89万元,则获得1万元奖金的员工有:
A.14人
B.19人
C.20人
D.21人
解析
第一步,本题考查基础应用题。
第二步,设获得10万元、5万元、1万元的人数分别为x、y、z人。根据总人数与总的奖金可列式:x+y+z=30①,10x+5y+z=89②,①×5-②可得4z-5x=61,由于5x的尾数只能是0或5,则4z的尾数只能是1或6,排除C、D选项。代入A选项,z=14,则x=(4×14-61)÷5<0,排除。
因此,选择B选项。
8.(单选题)甲、乙两个仓库共有货物102吨。如果从甲仓库调出3吨到乙仓库,那么甲仓库的货物正好是乙仓库的2倍。则甲仓库原有货物( )吨。
A.31
B.37
C.70
D.71
解析
解法一:
第一步,本题考查基础应用题,用方程法解题。
第二步,设甲仓库原有货物x吨,则乙仓库为(102-x)吨。根据甲是乙的2倍,可得x-3=2×(102-x+3),解得x=71。
因此,选择D选项。
解法二:
第一步,本题考查基础应用题。
第二步,容易判断甲仓库原有货物大于乙仓库,因此大于总数的一半51,排除A、B选项;甲减去3后是2的倍数,排除C选项。
因此,选择D选项。
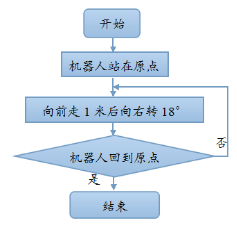
9.(单选题)科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为多少米?
A.20米
B.15米
C.12米
D.10米
解析
第一步,本题考查几何问题,属于几何特殊性质类。
第二步,机器人若想重新回到原点,需要旋转一周(360°)。由“每次向前一米右转18°”可知,需要右转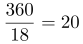 (次)才能回到原点,故共走了20×1=20(米)。
(次)才能回到原点,故共走了20×1=20(米)。
因此,选择A选项。
拓展
多边形外角和:所有多边形的外角和都为360°。
10.(单选题)水坝的横截面是一个梯形,它的面积为32.5平方米,高为5米,下底比上底的2倍多1米,梯形的上底是多少米?
A.6
B.4
C.5
D.7
解析
第一步,本题考查几何问题,属于平面几何类。用方程法解题。
第二步,设梯形的上底长度为x米,由下底比上底的2倍多1米,知下底长度为2x+1米。??
第三步,根据梯形的面积公式,得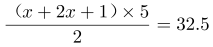 ,解得x=4(米)。
,解得x=4(米)。
因此,选择B选项。
?
A.20盆
B.21盆
C.40盆
D.41盆
解析
第一步,本题考查最值问题,属于最不利构造。
第二步,根据“至少……保证……”可知本题为最不利构造,答案为“所有最不利情况+1”。要求搬出的鲜花中一定有郁金香,最不利的情况是把所有月季花、牡丹花都搬出来,即搬出20+20=40(盆)。在此基础上再搬1盆,就能够保证搬出的鲜花中一定有郁金香,即至少要搬出40+1=41(盆)。
因此,选择D选项。
2.(单选题)某超市设有10个人工收银台。周末10个收银台全开,顾客结账平均排队20分钟。为提高效率,超市撤了4个人工收银台,并改造为6个自助收银台。若自助收银的效率是人工收银效率的90%。改造后,周末当人工收银台和自助收银台全开,预计顾客结账平均排队耗时约为?。
A.12分钟
B.14分钟
C.16分钟
D.18分钟
解析
第一步,本题考查工程问题效率类。
第二步,赋值每个人工收银台每分钟结账人数为1,那么总量=
每个自助收银台每分钟结账人数为0.9,那么
因此,选择D选项。
3.(单选题)甲租用乙的地种粮食,今年共收获3000斤粮食,包括大米、玉米和红薯。其中玉米800斤,红薯600斤。如果除租金之外,甲每年须将收获的大米的N%给乙作为回报,同时将红薯超过粮食总重的15%的部分也按照N%给乙作为回报,甲今年一共给乙210斤粮食,那么N%为多少?
A.8%
B.12%
C.14%
D.16%
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,根据共收获3000斤粮食,可得大米产量为3000-800-600=1600(斤),则甲每年给乙的大米为1600×N%。又根据红薯超过粮食总重的15%部分为600-3000×15%=150(斤),则甲每年给乙的红薯为150×N%。
第三步,根据共给乙210斤粮食,可列方程1600×N%+150×N%=210,解得N%=12%。
因此,选择B选项。
4.(单选题)一辆车从甲地行驶到乙地共20千米,用时20分钟,已知该车在匀加速到最大速度后开始匀减速,到乙地时速度恰好为0,问该车行驶的最大速度是多少千米/小时?
A.100
B.108
C.116
D.120
解析
第一步,本题考查基本行程类。
第二步,根据均加(减)速运动中,
因此,选择D选项。
5.(单选题)甲、乙两个仓库共存有340吨粮食。如果甲仓库存放的粮食是乙仓库的2倍多10吨,则甲仓库存有粮食( )吨。
A.110
B.120
C.230
D.240
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,设乙仓库粮食为x吨,则甲仓库粮食为2x+10吨。
第三步,根据题干甲、乙两个仓库共存有340吨粮食,列出等量关系:x+2x+10=340,求出x=110,则甲为230吨。
因此,选择C选项。
6.(单选题)如图所示,某地计划修建一个长50米、宽40米的长方形观光园。现在需要在观光园中修建几条鹅卵石小道供游客行走,其中一条是长为50米、宽为2米的水平直线型小路,另外两条修成斜线型,并且要求这两条斜线型小路任何地方的水平方向宽度都是1米,问修完小路后观光园剩下部分的面积是多少平方米?

A.1862
B.1880
C.1950
D.1960
解析
第一步,本题考查几何问题,属于平面几何类。
第二步,根据题意整个长方形观光园面积=50×40=2000(平方米)。其中水平直线型的小路面积=50×2=100(平方米),两条斜线型小路经过拼接可组合成一条底为1,高为38的平行四边形小路,面积=1×38=38(平方米)。
第三步,修完小路后观光园剩下部分的面积=2000-100-38=1862(平方米)。
因此,选择A选项。
7.(单选题)某企业年终评选了30名优秀员工,分三个等级,分别按每人10万元、5万元、1万元给与奖励。若共发放奖金89万元,则获得1万元奖金的员工有:
A.14人
B.19人
C.20人
D.21人
解析
第一步,本题考查基础应用题。
第二步,设获得10万元、5万元、1万元的人数分别为x、y、z人。根据总人数与总的奖金可列式:x+y+z=30①,10x+5y+z=89②,①×5-②可得4z-5x=61,由于5x的尾数只能是0或5,则4z的尾数只能是1或6,排除C、D选项。代入A选项,z=14,则x=(4×14-61)÷5<0,排除。
因此,选择B选项。
8.(单选题)甲、乙两个仓库共有货物102吨。如果从甲仓库调出3吨到乙仓库,那么甲仓库的货物正好是乙仓库的2倍。则甲仓库原有货物( )吨。
A.31
B.37
C.70
D.71
解析
解法一:
第一步,本题考查基础应用题,用方程法解题。
第二步,设甲仓库原有货物x吨,则乙仓库为(102-x)吨。根据甲是乙的2倍,可得x-3=2×(102-x+3),解得x=71。
因此,选择D选项。
解法二:
第一步,本题考查基础应用题。
第二步,容易判断甲仓库原有货物大于乙仓库,因此大于总数的一半51,排除A、B选项;甲减去3后是2的倍数,排除C选项。
因此,选择D选项。
9.(单选题)科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为多少米?

A.20米
B.15米
C.12米
D.10米
解析
第一步,本题考查几何问题,属于几何特殊性质类。
第二步,机器人若想重新回到原点,需要旋转一周(360°)。由“每次向前一米右转18°”可知,需要右转
因此,选择A选项。
拓展
多边形外角和:所有多边形的外角和都为360°。
10.(单选题)水坝的横截面是一个梯形,它的面积为32.5平方米,高为5米,下底比上底的2倍多1米,梯形的上底是多少米?
A.6
B.4
C.5
D.7
解析
第一步,本题考查几何问题,属于平面几何类。用方程法解题。
第二步,设梯形的上底长度为x米,由下底比上底的2倍多1米,知下底长度为2x+1米。??
第三步,根据梯形的面积公式,得
因此,选择B选项。
?










