1.(单选题)A、B两辆车同时从甲地出发驶向乙地,A车到达乙地后立即返回,返回途中与B车相遇,相遇点距乙地30公里,相遇后A车经过4小时返回甲地,B车经过0.5小时到达乙地,则A车往返一趟总共用了多少小时?
A.10
B.6+2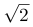
C.10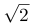
D.8+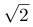
解析
解法一:
第一步,本题考查行程问题,属于相遇追及类。
第二步,设A、B两车相遇时间为t小时,B车的速度为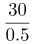 =60(km/h),相遇时乙车行驶路程60t,甲车行驶路程60t+30×2=60t+60,甲车的速度60t÷4=15t;两车相遇时,时间相同,路程与速度成正比,
=60(km/h),相遇时乙车行驶路程60t,甲车行驶路程60t+30×2=60t+60,甲车的速度60t÷4=15t;两车相遇时,时间相同,路程与速度成正比,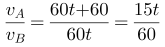 ,解得t=2+2
,解得t=2+2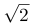 ,进而可得A车往返一趟总用时为4+t=6+2
,进而可得A车往返一趟总用时为4+t=6+2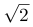 (小时)。
(小时)。
因此,选择B选项。
解法二:
第一步,本题考查行程问题,属于相遇追及类。
第二步,易知A的速度比B快,从甲地到相遇点A走了4小时,则往返一趟总用时一定大于8小时。又从相遇点到乙地B走了0.5小时,则A往返一趟一定小于(4+0.5)×2=9(小时),故总用时在8—9小时之间,只有B选项符合。
因此,选择B选项。
2.(单选题)某地的一种特色纪念品在旅游旺季十分畅销,有商家发现,进价为每个40元的纪念品,当售价定为44元时,每天可售出300个,售价每上涨1元,每天销量减少10个。现商家决定提价销售,若要使销售利润达到最大,则售价应为:
A.51
B.52
C.54
D.57
解析
第一步,本题考查经济利润问题。
第二步,设售价上涨了x个1元,则销量减少了10x个。那么根据总利润=单利×销量,可知总利润=(44-40+x)(300-10x)=10(4+x)(30-x)。此式在4+x=30-x时有最大值,此时x=13,则售价为44+13=57(元)。
因此,选择D选项。
3.(单选题)农户张某今年年初将一块长方形农田扩建为正方形农田,使得正方形边长与长方形的长相同,今年的农作物产量是去年的1.5倍。已知今年农作物亩产量比去年高20%,则原来长方形农田的长是宽的多少倍?
A.1.2
B.1.25
C.1.5
D.1.6
解析
第一步,本题考查几何问题。
第二步,设长方形的长、宽分别为x、y,则正方形的边长也为x,赋值原来的亩产量为10,则现在的亩产量为12。
第三步,总产量=亩产量×面积,根据今年农作物的产量是去年的1.5倍,则有12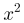 =1.5×10xy,解得x=1.25y。
=1.5×10xy,解得x=1.25y。
因此,选择B选项。
4.(单选题)A工程队的效率是B工程队的2倍,某工程交给两队共同完成需要6天。如果两队的工作效率均提高一倍,且B队中途休息了1天,问要保证工程按原来的时间完成,A队中途最多可以休息几天?
A.4
B.3
C.2
D.1
解析
第一步,本题考查工程问题,属于效率类,用赋值法解题。
第二步,赋值B队效率为1,则A队为2。根据两队共同完成需要6天,可得工程总量为(2+1)×6=18。
第三步,由工作效率均提高一倍,得B队效率变为2,A队变为4。设A队最多休息x天,得到18=4×(6-x)+2×(6-1),解得x=4。
因此,选择A选项。
5.(单选题)小王夜跑后回家喝水,往300毫升的杯子中倒入200毫升80℃热水和100毫升20℃凉水,发现依然太烫,无法喝下。于是接下来每次他都将水杯里的水倒去60毫升,加入同等体积的20℃凉水。假设在倒水过程中,水温没有流失,运动后人适宜的饮水温度范围是34~38℃,那么小王一共加了几次60毫升的凉水。
A.2
B.3
C.4
D.5
解析
第一步,本题考查溶液问题,属于溶液混合。
第二步,设小王将80℃热水和20℃凉水混合之后的温度为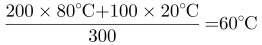 。同理第一次加入60毫升凉水之后的温度为
。同理第一次加入60毫升凉水之后的温度为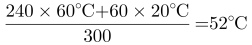 ,第二次加入60毫升凉水之后的温度为
,第二次加入60毫升凉水之后的温度为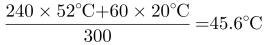 ,第三次加入60毫升凉水之后的温度为
,第三次加入60毫升凉水之后的温度为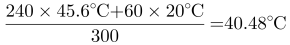 ,第四次加入60毫升凉水之后的温度为
,第四次加入60毫升凉水之后的温度为 。
。
第三步,可以发现在加入四次凉水后的温度在适宜饮水温度范围之间,故小王一共加了4次60毫升的凉水。
因此,选择C选项。
6.(单选题)A、B两台高性能计算机共同运行30小时可以完成某个计算任务。如两台计算机共同运行18小时后,A、B计算机分别抽调出20%和 50%的计算资源去执行其他任务,最后任务完成的时间会比预计时间晚6小时。如两台计算机共同运行18小时后,由B计算机单独运行,还需要多少小时才能完成该任务?
A.22
B.24
C.27
D.30
解析
第一步,本题考查工程问题,用方程法解题。
第二步,设A计算机的效率为5x,B计算机的效率为2y,则任务总量为(5x+2y)×30,共同运行18小时可以完成(5x+2y)×18,任务还剩(5x+2y)×12,由于A计算机抽调走20%即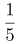 ,则A计算机此时效率变为4x,B计算机抽调走50%即
,则A计算机此时效率变为4x,B计算机抽调走50%即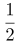 ,B计算机的此时效率为y,需要30-18+6=18(小时),可列方程:(5x+2y)×12=(4x+y)×18,解得y=2x,那么A计算机的效率为5x,B计算机的效率为4x,那么合作18小时后,剩下的工作B计算机单独完成需要
,B计算机的此时效率为y,需要30-18+6=18(小时),可列方程:(5x+2y)×12=(4x+y)×18,解得y=2x,那么A计算机的效率为5x,B计算机的效率为4x,那么合作18小时后,剩下的工作B计算机单独完成需要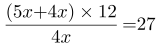 (小时)。
(小时)。
因此,选择C选项。
7.(单选题)两对夫妇各带一个小孩乘坐有6个座位的游览车,游览车每排只有1个座位。为安全起见,车的首尾两座一定要坐两位爸爸;两个小孩一定要排在一起。那么,这6人的排座方法有:
A.12种
B.24种
C.36种
D.48种
解析
第一步,本题考查排列组合问题,属于方法技巧类,用捆绑法解题。
第二步,先将两位爸爸安排在首尾两座,有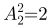 (种)方法;再将两个小孩看成一个整体,与两位妈妈一起排列,有
(种)方法;再将两个小孩看成一个整体,与两位妈妈一起排列,有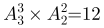 (种)方法。
(种)方法。
第三步,6人的排座方法共有2×12=24(种)方法。
因此,选择B选项。
8.(单选题)小明负责将某农场的鸡蛋运送到小卖部。按照规定,每送到1枚完整无损的鸡蛋,可得运费0.1元;若鸡蛋有损,不仅得不到该鸡蛋的运费,每破损一枚鸡蛋还要赔偿0.4元。小明10月份共运送鸡蛋25000枚,获得运费2480元。那么,在运送的过程中,鸡蛋破损了:
A.20枚
B.30枚
C.40枚
D.50枚
解析
解法一:
第一步,本题考查基础应用题,用方程法解题。
第二步,设破损枚数为x,可得(25000-x)×0.1-0.4x=2480,解得x=40。
因此,选择C选项。
解法二:
第一步,本题考查基础应用题。
第二步,假设25000枚鸡蛋全部完好无损,总共得到的运费为25000×0.1=2500(元),每破损一枚鸡蛋,不仅得不到该鸡蛋的运费0.1元,还要赔偿0.4元,共损失0.5元。则破损枚数为 (枚)。
(枚)。
因此,选择C选项。
9.(单选题)某学校组织活动进行队列训练,学生们组成一个25排的队列,后一排均比前一排多4个人,最后一排有125个学生。则这个队列一共有( )学生。
A.1925
B.1875
C.2010
D.1765
解析
解法一:
第一步,本题考查数列问题。
第二步,学生构成的数列是一个项数n为25,公差d为4,第25项为125的等差数列。首项 =
= -(25-1)×d=125-24×4=29,这个队列一共有
-(25-1)×d=125-24×4=29,这个队列一共有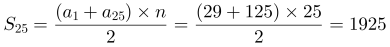 (个)学生。
(个)学生。
因此,选择A选项。
解法二:
第一步,本题考查数列问题。
第二步,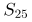 =中位数×项数=
=中位数×项数=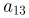 ×25=[125-(25-13)×4]×25=77×25=1925(个)学生。
×25=[125-(25-13)×4]×25=77×25=1925(个)学生。
因此,选择A选项。
10.(单选题)甲乙两人早上10点同时出发匀速向对方的工作单位行进,10点30分两人相遇并继续以原速度前行。10点54分甲到达乙的工作单位后,立刻原速返回自己单位。问甲返回自己单位时,乙已经到了甲的工作单位多长时间?
A.42分
B.40分30秒
C.43分30秒
D.45分
解析
第一步,本题考查行程问题,属于相遇追及类,用比例法解题。
第二步,根据10点同时出发,10点30分两人相遇,10点54分甲到达乙的工作单位,可知乙行进10:30-10:00=30(分钟)与甲行进10:54-10:30=24(分钟)的路程相等,故相同路程甲和乙的时间比为24∶30=4∶5。
第三步,甲单程用时54分钟,乙单程用时54÷4×5=67.5(分钟)。故甲返回自己单位时,乙已经到了甲的工作单位54×2-67.5=40.5(分钟),即40分钟30秒。
因此,选择B选项。
?
A.10
B.6+2
C.10
D.8+
解析
解法一:
第一步,本题考查行程问题,属于相遇追及类。
第二步,设A、B两车相遇时间为t小时,B车的速度为
因此,选择B选项。
解法二:
第一步,本题考查行程问题,属于相遇追及类。
第二步,易知A的速度比B快,从甲地到相遇点A走了4小时,则往返一趟总用时一定大于8小时。又从相遇点到乙地B走了0.5小时,则A往返一趟一定小于(4+0.5)×2=9(小时),故总用时在8—9小时之间,只有B选项符合。
因此,选择B选项。
2.(单选题)某地的一种特色纪念品在旅游旺季十分畅销,有商家发现,进价为每个40元的纪念品,当售价定为44元时,每天可售出300个,售价每上涨1元,每天销量减少10个。现商家决定提价销售,若要使销售利润达到最大,则售价应为:
A.51
B.52
C.54
D.57
解析
第一步,本题考查经济利润问题。
第二步,设售价上涨了x个1元,则销量减少了10x个。那么根据总利润=单利×销量,可知总利润=(44-40+x)(300-10x)=10(4+x)(30-x)。此式在4+x=30-x时有最大值,此时x=13,则售价为44+13=57(元)。
因此,选择D选项。
3.(单选题)农户张某今年年初将一块长方形农田扩建为正方形农田,使得正方形边长与长方形的长相同,今年的农作物产量是去年的1.5倍。已知今年农作物亩产量比去年高20%,则原来长方形农田的长是宽的多少倍?
A.1.2
B.1.25
C.1.5
D.1.6
解析
第一步,本题考查几何问题。
第二步,设长方形的长、宽分别为x、y,则正方形的边长也为x,赋值原来的亩产量为10,则现在的亩产量为12。
第三步,总产量=亩产量×面积,根据今年农作物的产量是去年的1.5倍,则有12
因此,选择B选项。
4.(单选题)A工程队的效率是B工程队的2倍,某工程交给两队共同完成需要6天。如果两队的工作效率均提高一倍,且B队中途休息了1天,问要保证工程按原来的时间完成,A队中途最多可以休息几天?
A.4
B.3
C.2
D.1
解析
第一步,本题考查工程问题,属于效率类,用赋值法解题。
第二步,赋值B队效率为1,则A队为2。根据两队共同完成需要6天,可得工程总量为(2+1)×6=18。
第三步,由工作效率均提高一倍,得B队效率变为2,A队变为4。设A队最多休息x天,得到18=4×(6-x)+2×(6-1),解得x=4。
因此,选择A选项。
5.(单选题)小王夜跑后回家喝水,往300毫升的杯子中倒入200毫升80℃热水和100毫升20℃凉水,发现依然太烫,无法喝下。于是接下来每次他都将水杯里的水倒去60毫升,加入同等体积的20℃凉水。假设在倒水过程中,水温没有流失,运动后人适宜的饮水温度范围是34~38℃,那么小王一共加了几次60毫升的凉水。
A.2
B.3
C.4
D.5
解析
第一步,本题考查溶液问题,属于溶液混合。
第二步,设小王将80℃热水和20℃凉水混合之后的温度为
第三步,可以发现在加入四次凉水后的温度在适宜饮水温度范围之间,故小王一共加了4次60毫升的凉水。
因此,选择C选项。
6.(单选题)A、B两台高性能计算机共同运行30小时可以完成某个计算任务。如两台计算机共同运行18小时后,A、B计算机分别抽调出20%和 50%的计算资源去执行其他任务,最后任务完成的时间会比预计时间晚6小时。如两台计算机共同运行18小时后,由B计算机单独运行,还需要多少小时才能完成该任务?
A.22
B.24
C.27
D.30
解析
第一步,本题考查工程问题,用方程法解题。
第二步,设A计算机的效率为5x,B计算机的效率为2y,则任务总量为(5x+2y)×30,共同运行18小时可以完成(5x+2y)×18,任务还剩(5x+2y)×12,由于A计算机抽调走20%即
因此,选择C选项。
7.(单选题)两对夫妇各带一个小孩乘坐有6个座位的游览车,游览车每排只有1个座位。为安全起见,车的首尾两座一定要坐两位爸爸;两个小孩一定要排在一起。那么,这6人的排座方法有:
A.12种
B.24种
C.36种
D.48种
解析
第一步,本题考查排列组合问题,属于方法技巧类,用捆绑法解题。
第二步,先将两位爸爸安排在首尾两座,有
第三步,6人的排座方法共有2×12=24(种)方法。
因此,选择B选项。
8.(单选题)小明负责将某农场的鸡蛋运送到小卖部。按照规定,每送到1枚完整无损的鸡蛋,可得运费0.1元;若鸡蛋有损,不仅得不到该鸡蛋的运费,每破损一枚鸡蛋还要赔偿0.4元。小明10月份共运送鸡蛋25000枚,获得运费2480元。那么,在运送的过程中,鸡蛋破损了:
A.20枚
B.30枚
C.40枚
D.50枚
解析
解法一:
第一步,本题考查基础应用题,用方程法解题。
第二步,设破损枚数为x,可得(25000-x)×0.1-0.4x=2480,解得x=40。
因此,选择C选项。
解法二:
第一步,本题考查基础应用题。
第二步,假设25000枚鸡蛋全部完好无损,总共得到的运费为25000×0.1=2500(元),每破损一枚鸡蛋,不仅得不到该鸡蛋的运费0.1元,还要赔偿0.4元,共损失0.5元。则破损枚数为
因此,选择C选项。
9.(单选题)某学校组织活动进行队列训练,学生们组成一个25排的队列,后一排均比前一排多4个人,最后一排有125个学生。则这个队列一共有( )学生。
A.1925
B.1875
C.2010
D.1765
解析
解法一:
第一步,本题考查数列问题。
第二步,学生构成的数列是一个项数n为25,公差d为4,第25项为125的等差数列。首项
 =
= -(25-1)×d=125-24×4=29,这个队列一共有
-(25-1)×d=125-24×4=29,这个队列一共有因此,选择A选项。
解法二:
第一步,本题考查数列问题。
第二步,
因此,选择A选项。
10.(单选题)甲乙两人早上10点同时出发匀速向对方的工作单位行进,10点30分两人相遇并继续以原速度前行。10点54分甲到达乙的工作单位后,立刻原速返回自己单位。问甲返回自己单位时,乙已经到了甲的工作单位多长时间?
A.42分
B.40分30秒
C.43分30秒
D.45分
解析
第一步,本题考查行程问题,属于相遇追及类,用比例法解题。
第二步,根据10点同时出发,10点30分两人相遇,10点54分甲到达乙的工作单位,可知乙行进10:30-10:00=30(分钟)与甲行进10:54-10:30=24(分钟)的路程相等,故相同路程甲和乙的时间比为24∶30=4∶5。
第三步,甲单程用时54分钟,乙单程用时54÷4×5=67.5(分钟)。故甲返回自己单位时,乙已经到了甲的工作单位54×2-67.5=40.5(分钟),即40分钟30秒。
因此,选择B选项。
?










